Grafo assimétrico

Famílias de grafos definidos por seus automorfismos
distância-transitivo	${\displaystyle \rightarrow }$	distância-regular	${\displaystyle \leftarrow }$	fortemente regular
${\displaystyle \downarrow }$
simétrico (arco-transitivo)	${\displaystyle \leftarrow }$	t-transitivo, t ≥ 2		.
${\displaystyle \downarrow }$ (se conectado)
transitivo nos vértices e nas arestas	${\displaystyle \rightarrow }$	aresta-transitivo e regular	${\displaystyle \rightarrow }$	aresta-transitivo
${\displaystyle \downarrow }$		${\displaystyle \downarrow }$
vértice-transitivo	${\displaystyle \rightarrow }$	regular
${\displaystyle \uparrow }$
grafo de Cayley		antissimétrico		assimétrico

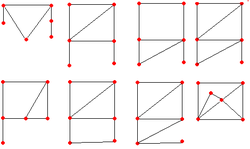
No campo da matemática da teoria dos grafos, um grafo não direcionado é chamado um grafo assimétrico se não tiver simetrias não triviais.

Formalmente, um automorfismo de um grafo é uma permutação p de seus vértices com a propriedade que quaisquer dois vértices u e v são adjacentes se e somente se p(u) e p(v) são adjacentes. O mapeamento identidade de um grafo em si é sempre um automorfismo, e é chamado de automorfismo trivial do grafo. Um grafo assimétrico é um grafo para os quais não existem outros automorfismos.

O menor grafo não trivial assimétrico tem 6 vértices.^[1] O menor grafo regular assimétrico têm dez vértices; existem grafos assimétricos de dez vértices são 4-regulares e 5-regulares.^[2][3]

O menor grafo cúbico assimétrico é o grafo de Frucht de doze vértices descoberto em 1939.^[4] De acordo com uma versão reforçada do teorema de Frucht, há infinitamente mais grafos cúbicos assimétricos.

A classe de grafos assimétrica é fechada em complementos: um grafo G é assimétrico se e somente se seu complemento o é.^[1] Qualquer grafo assimétrico de n-vértices pode ser feito simétrico, adicionando e removendo um total de, no máximo n/2 + o(n) arestas.^[1]

A proporção de grafos sobre n vértices com automorfismo não trivial tende a zero a medida que n cresce, que é informalmente expressado como "quase todos grafos finitos são assimétricos". Em contraste, uma vez mais informalmente, "quase todos os grafos infinitos são simétricos". Mais especificamente, grafos aleatórios infinitos e contáveis no modelo Erdős–Rényi são, com probabilidade 1, isomórficos ao altamente simétrico grafo Rado.^[1]

A menor árvore assimétrica tem sete vértices: consiste de três caminhos de comprimentos de 1, 2 e 3, ligados a um terminal comum^[5] Em contraste com a situação dos grafos, quase todas as árvores são simétricas. Em particular, se uma árvore é escolhida de forma uniforme aleatoriamente entre todas as árvores em n nós rotulados, em seguida, com probabilidade tendendo a 1 quando n aumenta, a árvore terá cerca de duas folhas adjacentes ao mesmo nó e terá simetrias trocando entre essas duas folhas.^[1]

Referências