HSV

 Nota: Para outros significados, veja HSV (desambiguação).

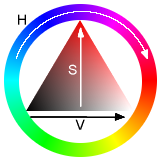
HSV é a abreviatura para o sistema de cores formadas pelas componentes hue (matiz), saturation (saturação) e value (valor). O HSV também é conhecido como HSB (hue, saturation e brightness — matiz, saturação e brilho, respectivamente). Esse sistema de cores define o espaço de cor conforme descrito abaixo, utilizando seus três parâmetros:

• Matiz (tonalidade): Verifica o tipo de cor, abrangendo todas as cores do espectro, desde o vermelho até o violeta, mais o magenta. Atinge valores de 0 a 360, mas para algumas aplicações, esse valor é normalizado de 0 a 100%.
• Saturação: Também chamado de "pureza". Quanto menor esse valor, mais com tom de cinza aparecerá a imagem. Quanto maior o valor, mais "pura" é a imagem. Atinge valores de 0 a 100%.
• Valor (brilho): Define o brilho da cor. Atinge valores de 0 a 100%.

Este sistema foi inventado no ano de 1974, por Alvy Ray Smith. É caracterizada por ser uma transformação não-linear do sistema de cores RGB. Outros sistemas de cores relacionados incluem o HSL (L de luminosity ou luminosidade) e o HSI (I de intensity ou intensidade).

Seja uma cor definida por (R, G, B), onde R, G e B estão entre 0.0 e 1.0, onde 0.0 e 1.0 são, respectivamente, o maior e o menor valor possível para cada. A transformação para os parâmetros (H, S, V) dessa cor pode ser determinada pelas fórmulas abaixo.

Seja MAX e MIN os valores máximo e mínimo, respectivamente, dos valores (R, G, B):

${\displaystyle H={\begin{cases}60\times {\frac {G-B}{MAX-MIN}}+0,&{\mbox{if }}MAX=R\\&{\mbox{and }}G\geq B\\60\times {\frac {G-B}{MAX-MIN}}+360,&{\mbox{if }}MAX=R\\&{\mbox{and }}G<B\\60\times {\frac {B-R}{MAX-MIN}}+120,&{\mbox{if }}MAX=G\\60\times {\frac {R-G}{MAX-MIN}}+240,&{\mbox{if }}MAX=B\end{cases}}}$

${\displaystyle S={\begin{cases}{\frac {MAX-MIN}{MAX}}&{\mbox{if }}MAX>0\\0&{\mbox{if }}MAX=0\end{cases}}}$

${\displaystyle V=MAX\,}$

Os resultados dão a tonalidade variando de 0 a 360, indicando o ângulo no circulo aonde a tonalidade (H) está definido, e a saturação e o brilho variando de 0.0 a 1.0, representando o menor e o maior valor possível.

Seja uma cor definida por (H, S, V), onde H, varia de 0.0 a 360.0, informando o ângulo, em graus, no circulo onde esse parâmentro está definido, e com S e V variando de 0.0 a 1.0. A transformação para os parâmetros (R, G, B) desta cor podem ser calculados conforme as fórmulas abaixo:

• Primeiramente, se S = 0, o resultado será cinza. Para este caso, os valores de R, G e B são iguais a V e, o valor de H é irrelevante.
• Para S diferente de zero, as fórmulas abaixo são aplicáveis:

${\displaystyle H_{i}=\left\lfloor {H \over 60}\right\rfloor \mod 6}$

${\displaystyle f={H \over 60}-H_{i}}$

${\displaystyle p=V(1-S)\,}$

${\displaystyle q=V(1-fS)\,}$

${\displaystyle t=V(1-(1-f)S)\,}$

${\displaystyle {\mbox{if }}H_{i}=0\rightarrow R=V,G=t,B=p\,}$

${\displaystyle {\mbox{if }}H_{i}=1\rightarrow R=q,G=V,B=p\,}$

${\displaystyle {\mbox{if }}H_{i}=2\rightarrow R=p,G=V,B=t\,}$

${\displaystyle {\mbox{if }}H_{i}=3\rightarrow R=p,G=q,B=V\,}$

${\displaystyle {\mbox{if }}H_{i}=4\rightarrow R=t,G=p,B=V\,}$

${\displaystyle {\mbox{if }}H_{i}=5\rightarrow R=V,G=p,B=q\,}$

Estas fórmulas, dão R, G e B variando de 0.0 a 1.0.

• CMYK
• RGB
• Teoria das cores

Referências