Quadrilátero

Aspeto mover para a barra lateral ocultar

Esta página ou se(c)ção precisa ser formatada para o padrão wiki. Por favor ajude a formatar esta página de acordo com as diretrizes estabelecidas. (Maio de 2015)

Em geometria plana euclidiana, quadrilátero é um polígono simples de quatro lados. A soma dos seus ângulos internos é igual a 360 ∘ , {\displaystyle 360^{\circ },} $360^{\circ },$ bem como a soma dos seus ângulos externos.

Definição

Sejam A {\displaystyle A} $A$ , B {\displaystyle B} $B$ , C {\displaystyle C} $C$ e D {\displaystyle D} $D$ quatro pontos de um mesmo plano, todos distintos e três não colineares. Se os segmentos A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ , B C ¯ {\displaystyle {\overline {BC}}} ${\overline {BC}}$ , C D ¯ {\displaystyle {\overline {CD}}} ${\overline {CD}}$ e D A ¯ {\displaystyle {\overline {DA}}} ${\overline {DA}}$ interceptam-se apenas nas extremidades, a reunião desses quatro segmentos é um quadrilátero.

Logo, podemos definir da seguinte forma:

Quadrilátero A B C D {\displaystyle ABCD} $ABCD$ é definido como a união A B ¯ ∪ B C ¯ ∪ C D ¯ ∪ D A ¯ {\displaystyle {\overline {AB}}\cup {\overline {BC}}\cup {\overline {CD}}\cup {\overline {DA}}} ${\overline {AB}}\cup {\overline {BC}}\cup {\overline {CD}}\cup {\overline {DA}}$

Um quadrilátero.

Elementos

Elementos de um quadrilátero

Identificamos os seguintes elementos em um quadrilátero A B C D : {\displaystyle ABCD:} $ABCD:$

vértices: os pontos A , {\displaystyle A,} $A,$ B , {\displaystyle B,} $B,$ C {\displaystyle C} $C$ e D ; {\displaystyle D;} $D;$
lados: os segmentos de reta A B ¯ , {\displaystyle {\overline {AB}},} ${\overline {AB}},$ B C ¯ , {\displaystyle {\overline {BC}},} ${\overline {BC}},$ C D ¯ {\displaystyle {\overline {CD}}} ${\overline {CD}}$ e D A ¯ ; {\displaystyle {\overline {DA}};} ${\overline {DA}};$
diagonais: A diagonal de um polígono é um segmento cujas extremidades são vértices não consecutivos do polígono, portanto os segmentos A C ¯ {\displaystyle {\overline {AC}}} ${\overline {AC}}$ e B D ¯ {\displaystyle {\overline {BD}}} ${\overline {BD}}$ são chamados de diagonais do quadrilátero A B C D {\displaystyle ABCD} $ABCD$ .
ângulos internos: os ângulos D A ^ B ( a ^ ) , {\displaystyle D{\hat {A}}B({\hat {a}}),} $D{\hat {A}}B({\hat {a}}),$ A B ^ C ( b ^ ) , {\displaystyle A{\hat {B}}C({\hat {b}}),} $A{\hat {B}}C({\hat {b}}),$ B C ^ D ( c ^ ) , {\displaystyle B{\hat {C}}D({\hat {c}}),} $B{\hat {C}}D({\hat {c}}),$ C D ^ A ( d ^ ) ; {\displaystyle C{\hat {D}}A({\hat {d}});} $C{\hat {D}}A({\hat {d}});$
Os ângulos e ^ , {\displaystyle {\hat {e}},} ${\hat {e}},$ f ^ , {\displaystyle {\hat {f}},} ${\hat {f}},$ g ^ {\displaystyle {\hat {g}}} ${\hat {g}}$ e h ^ {\displaystyle {\hat {h}}} ${\hat {h}}$ são os ângulos externos do quadrilátero.

Cada ângulo interno de um quadrilátero tem por suplemento o seu respectivo ângulo externo.

e ^ {\displaystyle {\hat {e}}} ${\hat {e}}$ é o suplemento do ângulo a ^ {\displaystyle {\hat {a}}} ${\hat {a}}$
f ^ {\displaystyle {\hat {f}}} ${\hat {f}}$ é o suplemento do ângulo b ^ {\displaystyle {\hat {b}}} ${\hat {b}}$
g ^ {\displaystyle {\hat {g}}} ${\hat {g}}$ é o suplemento do ângulo c ^ {\displaystyle {\hat {c}}} ${\hat {c}}$
h ^ {\displaystyle {\hat {h}}} ${\hat {h}}$ é o suplemento do ângulo d ^ {\displaystyle {\hat {d}}} ${\hat {d}}$

Quadriláteros notáveis

Os quadriláteros notáveis são os trapézios, os paralelogramos, os retângulos, os losangos e os quadrados.

Trapézio

Um quadrilátero plano convexo é um trapézio se, e somente se, possui dois lados paralelos.

Paralelogramo ABCD.

A B C D é trapézio ⟺ ( A B ¯ / / C D ¯ ou A D ¯ / / B C ¯ ) {\displaystyle ABCD\quad {\text{é trapézio }}\qquad \Longleftrightarrow \qquad \left({\overline {AB}}//{\overline {CD}}\quad {\text{ou}}\quad {\overline {AD}}//{\overline {BC}}\right)} $ABCD\quad {\text{é trapézio }}\qquad \Longleftrightarrow \qquad \left({\overline {AB}}//{\overline {CD}}\quad {\text{ou}}\quad {\overline {AD}}//{\overline {BC}}\right)$

Paralelogramo

Um quadrilátero plano convexo é um paralelogramo se, e somente se, possui os lados opostos paralelos.

A B C D é paralelogramo ⟺ ( A B ¯ / / C D ¯ e A D ¯ / / B C ¯ ) {\displaystyle ABCD\quad {\text{é paralelogramo }}\qquad \Longleftrightarrow \qquad \left({\overline {AB}}//{\overline {CD}}\quad {\text{e}}\quad {\overline {AD}}//{\overline {BC}}\right)} $ABCD\quad {\text{é paralelogramo }}\qquad \Longleftrightarrow \qquad \left({\overline {AB}}//{\overline {CD}}\quad {\text{e}}\quad {\overline {AD}}//{\overline {BC}}\right)$

Retângulo

Um quadrilátero plano convexo é um retângulo se, e somente se, possui os quatro ângulo congruentes.

A B C D é retângulo ⟺ A ^ ≡ B ^ ≡ C ^ ≡ D ^ {\displaystyle ABCD\quad {\text{é retângulo }}\qquad \Longleftrightarrow \qquad {{\hat {A}}\equiv {\hat {B}}\equiv {\hat {C}}\equiv {\hat {D}}}} $ABCD\quad {\text{é retângulo }}\qquad \Longleftrightarrow \qquad {{\hat {A}}\equiv {\hat {B}}\equiv {\hat {C}}\equiv {\hat {D}}}$

Retângulo, losango e quadrado.

Losango

Um quadrilátero plano convexo é um losango se, e somente se, possui os quatro lados congruentes.

A B C D é losango ⟺ A B ¯ ≡ B C ¯ ≡ C D ¯ ≡ D A ¯ {\displaystyle ABCD\quad {\text{é losango }}\qquad \Longleftrightarrow \qquad {{\overline {AB}}\equiv {\overline {BC}}\equiv {\overline {CD}}\equiv {\overline {DA}}}} $ABCD\quad {\text{é losango }}\qquad \Longleftrightarrow \qquad {{\overline {AB}}\equiv {\overline {BC}}\equiv {\overline {CD}}\equiv {\overline {DA}}}$

Quadrado

Um quadrilátero plano convexo é um quadrado se, e somente se, possui os quatro ângulos congruentes e os quatro lados congruentes.os quatro lados possuem a mesma medida

A B C D é quadrado ⟺ A ^ ≡ B ^ ≡ C ^ ≡ D ^ e A B ¯ ≡ B C ¯ ≡ C D ¯ ≡ D A ¯ {\displaystyle ABCD\quad {\text{é quadrado }}\qquad \Longleftrightarrow \qquad {{\hat {A}}\equiv {\hat {B}}\equiv {\hat {C}}\equiv {\hat {D}}}\quad {\text{e}}\quad {{\overline {AB}}\equiv {\overline {BC}}\equiv {\overline {CD}}\equiv {\overline {DA}}}} $ABCD\quad {\text{é quadrado }}\qquad \Longleftrightarrow \qquad {{\hat {A}}\equiv {\hat {B}}\equiv {\hat {C}}\equiv {\hat {D}}}\quad {\text{e}}\quad {{\overline {AB}}\equiv {\overline {BC}}\equiv {\overline {CD}}\equiv {\overline {DA}}}$

Soma dos ângulos de um quadrilátero

Em um quadrilátero, tanto a soma das medidas dos ângulos internos quanto a soma dos ângulos externos são iguais a 360 ∘ {\displaystyle 360^{\circ }} $360^{\circ }$ .

Assim, seja A B C D {\displaystyle ABCD} $ABCD$ um quadrilátero qualquer, cujos ângulos internos medem a {\displaystyle a} $a$ , b {\displaystyle b} $b$ , c {\displaystyle c} $c$ e d {\displaystyle d} $d$ e seus ângulos externos, respectivamente e {\displaystyle e} $e$ , f {\displaystyle f} $f$ , g {\displaystyle g} $g$ e h {\displaystyle h} $h$ , temos:

a + b + c + d = 360 ∘ {\displaystyle a+b+c+d=360^{\circ }} $a+b+c+d=360^{\circ }$ e e + f + g + h = 360 ∘ {\displaystyle e+f+g+h=360^{\circ }} $e+f+g+h=360^{\circ }$

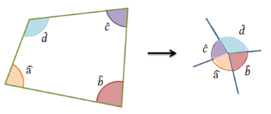Ilustração da soma dos ângulos internos de um quadrilátero. Figura 9

Demonstração

Para demonstrar essa propriedade vamos traçar a diagonal A C ¯ {\displaystyle {\overline {AC}}} ${\overline {AC}}$ (sem perda de generalidade), de modo a decompor o quadrilátero em dois triângulos, △ A B C {\displaystyle \triangle {ABC}} $\triangle {ABC}$ e △ A C D {\displaystyle \triangle {ACD}} $\triangle {ACD}$ .

Como a soma dos ângulos internos de um triângulo é 180 ∘ {\displaystyle 180^{\circ }} $180^{\circ }$ , temos:

△ A B C {\displaystyle \triangle {ABC}} $\triangle {ABC}$ : a ′ + b + c ′ = 180 ∘ {\displaystyle a'+b+c'=180^{\circ }} $a'+b+c'=180^{\circ }$

△ A C D {\displaystyle \triangle {ACD}} $\triangle {ACD}$ : a ″ + c ″ + d = 180 ∘ {\displaystyle a''+c''+d=180^{\circ }} $a''+c''+d=180^{\circ }$

Assim, se somarmos as duas equações acima, obtemos:

a ′ + a ″ + b + d + c ′ + c ″ = 360 ∘ ⟺ a + b + c + d = 360 ∘ {\displaystyle a'+a''+b+d+c'+c''=360^{\circ }\qquad \Longleftrightarrow \qquad {a+b+c+d=360^{\circ }}} $a'+a''+b+d+c'+c''=360^{\circ }\qquad \Longleftrightarrow \qquad {a+b+c+d=360^{\circ }}$

Sabemos que cada ângulo interno é suplementar ao seu interno adjacente. Assim temos:

a = 180 ∘ − e {\displaystyle a=180^{\circ }-e} $a=180^{\circ }-e$

b = 180 ∘ − f {\displaystyle b=180^{\circ }-f} $b=180^{\circ }-f$

c = 180 ∘ − g {\displaystyle c=180^{\circ }-g} $c=180^{\circ }-g$

d = 180 ∘ − h {\displaystyle d=180^{\circ }-h} $d=180^{\circ }-h$

Ou seja:

180 ∘ − e + 180 ∘ − f + 180 ∘ − g + 180 ∘ − h = 360 ∘ ⟺ e + f + g + h = 360 ∘ − 360 ∘ + 360 ∘ {\displaystyle 180^{\circ }-e+180^{\circ }-f+180^{\circ }-g+180^{\circ }-h=360^{\circ }\qquad \Longleftrightarrow \qquad {e+f+g+h=360^{\circ }-360^{\circ }+360^{\circ }}} $180^{\circ }-e+180^{\circ }-f+180^{\circ }-g+180^{\circ }-h=360^{\circ }\qquad \Longleftrightarrow \qquad {e+f+g+h=360^{\circ }-360^{\circ }+360^{\circ }}$

Logo

e + f + g + h = 360 ∘ {\displaystyle e+f+g+h=360^{\circ }} $e+f+g+h=360^{\circ }$ .

Quadriláteros Côncavos e Convexos

Os quadriláteros são classificados em quadriláteros convexos ou côncavos. Um quadrilátero é convexo quando a região plana limitada por seus lados é convexa, caso contrário ele é côncavo.

Uma outra forma de definir quadriláteros convexos e côncavos é a seguinte:

Um polígono é convexo se a reta que contém qualquer de seus lados deixa todos os demais lados no mesmo semiplano. De forma contrária, um polígono é côncavo se existe uma reta que contém um de seus lados e deixa parte dos demais lados num semiplano e parte no outro semiplano. (figura 11)

Quadriláteros côncavos e convexos.

Dentre os quadriláteros convexos existem dois grupos que se destacam: os trapézios e os paralelogramos.

Área dos Quadriláteros Notáveis

Área do trapézio

A = ( B + b ) . h 2 {\displaystyle A={\dfrac {(B+b).h}{2}}} $A={\dfrac {(B+b).h}{2}}$

onde, B é a base maior do trapézio; b é a base menor do trapézio; h é a altura do trapézio.

Área dos paralelogramos

A = b . h {\displaystyle A=b.h} $A=b.h$

onde, b é a base do paralelogramo; h é a altura do paralelogramo. Como todo retângulo, losango e quadrado é um paralelogramo, o calculo de sua área é feito da mesma forma.

Área dos paralelogramos

Considere D e d a diagonal maior e a diagonal menor do losango, respectivamente. Note que a área do losango é a metade da área de um retângulo cujos lados são as respectivas diagonais do losango.

Quadrilátero circunscrito

Um quadrilátero convexo é circunscritível a uma circunferência se, e somente se, seus quatro lados são tangentes a circunferência.

Propriedade

Quadrilátero A B C D {\displaystyle ABCD}

ABCD

circunscrito à circunferência.

Um quadrilátero só é circunscritível a uma circunferência se a soma de quaisquer dois lados opostos é igual a soma dos outros dois lados opostos.

Isso pode ser enunciado através do seguinte teorema:

"Uma condição necessária e suficiente para um quadrilátero convexo ser circunscritível a uma circunferência é a soma de dois lados opostos ser igual à soma dos outros dois."

Por se tratar de uma equivalência, precisamos demonstrar esse teorema em duas partes.

Primeira parte

Se um quadrilátero convexo é circunscrito a uma circunferência, a soma de dois lados opostos é igual à soma dos outros dois.

Assim, queremos mostrar que:

A B C D circunscrito a λ ⟹ A B ¯ + C D ¯ = A D ¯ + B C ¯ {\displaystyle ABCD\quad {\text{circunscrito a }}\quad \lambda \qquad \Longrightarrow \qquad {{\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}}} $ABCD\quad {\text{circunscrito a }}\quad \lambda \qquad \Longrightarrow \qquad {{\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}}$

Sejam X {\displaystyle X} $X$ , Y {\displaystyle Y} $Y$ , Z {\displaystyle Z} $Z$ e T {\displaystyle T} $T$ os pontos de tangência de A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ , B C ¯ {\displaystyle {\overline {BC}}} ${\overline {BC}}$ , C D ¯ {\displaystyle {\overline {CD}}} ${\overline {CD}}$ e D A ¯ {\displaystyle {\overline {DA}}} ${\overline {DA}}$ , respectivamente, e, aplicando as propriedades dos segmentos tangentes, temos:

A X ¯ ≡ A T ¯ {\displaystyle {\overline {AX}}\equiv {\overline {AT}}} ${\overline {AX}}\equiv {\overline {AT}}$ , B X ¯ ≡ B Y ¯ {\displaystyle {\overline {BX}}\equiv {\overline {BY}}} ${\overline {BX}}\equiv {\overline {BY}}$ , C Z ¯ ≡ C Y ¯ {\displaystyle {\overline {CZ}}\equiv {\overline {CY}}} ${\overline {CZ}}\equiv {\overline {CY}}$ e D Z ¯ ≡ D T ¯ {\displaystyle {\overline {DZ}}\equiv {\overline {DT}}} ${\overline {DZ}}\equiv {\overline {DT}}$ .

Se somarmos as quatro equações, teremos:

A X ¯ + B X ¯ + C Z ¯ + D Z ¯ = A T ¯ + B Y ¯ + C Y ¯ + D T ¯ {\displaystyle {\color {blue}{\overline {AX}}}+{\color {blue}{\overline {BX}}}+{\color {red}{\overline {CZ}}}+{\color {red}{\overline {DZ}}}={\color {green}{\overline {AT}}}+{\color {YellowOrange}{\overline {BY}}}+{\color {YellowOrange}{\overline {CY}}}+{\color {green}{\overline {DT}}}} ${\color {blue}{\overline {AX}}}+{\color {blue}{\overline {BX}}}+{\color {red}{\overline {CZ}}}+{\color {red}{\overline {DZ}}}={\color {green}{\overline {AT}}}+{\color {YellowOrange}{\overline {BY}}}+{\color {YellowOrange}{\overline {CY}}}+{\color {green}{\overline {DT}}}$

Isso é equivalente a dizer:

A B ¯ + C D ¯ = A D ¯ + B C ¯ {\displaystyle {\color {blue}{\overline {AB}}}+{\color {red}{\overline {CD}}}={\color {green}{\overline {AD}}}+{\color {YellowOrange}{\overline {BC}}}} ${\color {blue}{\overline {AB}}}+{\color {red}{\overline {CD}}}={\color {green}{\overline {AD}}}+{\color {YellowOrange}{\overline {BC}}}$ .

Segunda parte

Se num quadrilátero convexo a soma de dois lados opostos é igual à soma dos outros dois, então o quadrilátero é circunscritível a uma circunferência.

Imagem suporte para demonstração

Assim, queremos mostrar que:

A B ¯ + C D ¯ = A D ¯ + B C ¯ ⟹ A B C D é circunscritível a uma circunferência {\displaystyle {{\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}}\qquad \Longrightarrow \qquad {ABCD}\quad {\text{é circunscritível a uma circunferência}}} ${{\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}}\qquad \Longrightarrow \qquad {ABCD}\quad {\text{é circunscritível a uma circunferência}}$

Para demonstrar essa propriedade começaremos por enunciar que A B C D {\displaystyle ABCD} $ABCD$ não é circunscritível e, então, encontraremos uma contradição.

Assim, tomaremos uma circunferência λ {\displaystyle \lambda } $\lambda$ tangente aos lados A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ , B C ¯ {\displaystyle {\overline {BC}}} ${\overline {BC}}$ e C D ¯ {\displaystyle {\overline {CD}}} ${\overline {CD}}$ do quadrilátero.

Imagem suporte para demonstração

Como enunciamos que A B C D {\displaystyle ABCD} $ABCD$ não é circunscritível a λ {\displaystyle \lambda } $\lambda$ , existe um quadrilátero A B C X {\displaystyle ABCX} $ABCX$ , com X {\displaystyle X} $X$ na reta C D ↔ {\displaystyle {\overleftrightarrow {CD}}} ${\overleftrightarrow {CD}}$ que é circunscrito a λ {\displaystyle \lambda } $\lambda$ .

Visto que A B C X {\displaystyle ABCX} $ABCX$ é circunscrito a λ {\displaystyle \lambda } $\lambda$ , temos, conforme foi demonstrado acima:

A B ¯ + C X ¯ = B C ¯ + A X ¯ {\displaystyle {\overline {AB}}+{\overline {CX}}={\overline {BC}}+{\overline {AX}}} ${\overline {AB}}+{\overline {CX}}={\overline {BC}}+{\overline {AX}}$ .

Por hipótese, temos: A B ¯ + C D ¯ = A D ¯ + B C ¯ {\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}} ${\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}$ .

Note que X {\displaystyle X} $X$ está sob a reta C D ↔ {\displaystyle {\overleftrightarrow {CD}}} ${\overleftrightarrow {CD}}$ , ou seja, precisamos admitir, sem perda de rigor, que X {\displaystyle X} $X$ pode estar ou sob o segmento C D ¯ {\displaystyle {\overline {CD}}} ${\overline {CD}}$ ou fora dele.

Para cada um dos casos temos:

X ∈ C D ¯ ⟹ C X ¯ + X D ¯ = C D ¯ {\displaystyle X\in {\overline {CD}}\qquad \Longrightarrow \qquad {{\overline {CX}}+{\overline {XD}}={\overline {CD}}}} $X\in {\overline {CD}}\qquad \Longrightarrow \qquad {{\overline {CX}}+{\overline {XD}}={\overline {CD}}}$
X ∉ C D ¯ ⟹ C X ¯ − X D ¯ = C D ¯ {\displaystyle X\notin {\overline {CD}}\qquad \Longrightarrow \qquad {\overline {CX}}-{\overline {XD}}={\overline {CD}}} $X\notin {\overline {CD}}\qquad \Longrightarrow \qquad {\overline {CX}}-{\overline {XD}}={\overline {CD}}$

No primeiro caso, temos:

A B ¯ + C D ¯ = A D ¯ + B C ¯ ⟹ A B ¯ + C X ¯ + X D ¯ = A D ¯ + B C ¯ ⟹ A B ¯ + C X ¯ = A D ¯ + B C ¯ − X D ¯ {\displaystyle {\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}\qquad \Longrightarrow \qquad {\overline {AB}}+{\overline {CX}}+{\overline {XD}}={\overline {AD}}+{\overline {BC}}\qquad \Longrightarrow \qquad {{\overline {AB}}+{\overline {CX}}={\overline {AD}}+{\overline {BC}}-{\overline {XD}}}} ${\overline {AB}}+{\overline {CD}}={\overline {AD}}+{\overline {BC}}\qquad \Longrightarrow \qquad {\overline {AB}}+{\overline {CX}}+{\overline {XD}}={\overline {AD}}+{\overline {BC}}\qquad \Longrightarrow \qquad {{\overline {AB}}+{\overline {CX}}={\overline {AD}}+{\overline {BC}}-{\overline {XD}}}$

Como, anteriormente vimos que A B ¯ + C X ¯ = B C ¯ + A X ¯ {\displaystyle {\overline {AB}}+{\overline {CX}}={\overline {BC}}+{\overline {AX}}} ${\overline {AB}}+{\overline {CX}}={\overline {BC}}+{\overline {AX}}$ , obtemos:

B C ¯ + A X ¯ = A D ¯ + B C ¯ − X D ¯ ⟹ A X ¯ = A D ¯ + X D ¯ {\displaystyle {\overline {BC}}+{\overline {AX}}={\overline {AD}}+{\overline {BC}}-{\overline {XD}}\qquad \Longrightarrow \qquad {{\overline {AX}}={\overline {AD}}+{\overline {XD}}}} ${\overline {BC}}+{\overline {AX}}={\overline {AD}}+{\overline {BC}}-{\overline {XD}}\qquad \Longrightarrow \qquad {{\overline {AX}}={\overline {AD}}+{\overline {XD}}}$

Porém, observe que essa última relação é um absurdo, pois contradiz a existência de △ A D X {\displaystyle \triangle {ADX}} $\triangle {ADX}$ , fazendo com que X = D {\displaystyle X=D} $X=D$ .

Logo, para esse primeiro caso temos que A B C D {\displaystyle ABCD} $ABCD$ é circunscritível a uma circunferência.

O segundo caso prova-se de modo análogo, fazendo relações algébricas similares de modo a obter que A X ¯ = A D ¯ − X D ¯ {\displaystyle {\overline {AX}}={\overline {AD}}-{\overline {XD}}} ${\overline {AX}}={\overline {AD}}-{\overline {XD}}$ , o que também obriga ser verdadeiro X = D {\displaystyle X=D} $X=D$ .

Portanto, podemos afirmar que, se num quadrilátero convexo a soma de dois lados opostos é igual à soma dos outros dois, então o quadrilátero é circunscritível a uma circunferência.

As Definições de Quadriláteros ao Longo da História

Os Elementos de Euclides

Os Elementos de Euclides foi um dos mais antigos tratados gregos existentes; a mais renomada obra na história da matemática. Segundo Proclus tal obra está relacionada com o resto da matemática, assim como as letras do alfabeto estão relacionadas com a linguagem. Euclides em sua obra, “Os Elementos”, livro I, Definições, admite as seguintes definições para as figuras quadriláteros:

Rombóide é a que tem tanto os lados opostos quanto os ângulos opostos iguais entre si, a qual não é equilátera nem retangular (p. 98). Ser retangular para Euclides é ter cada um dos ângulos opostos reto
Das áreas paralelogrâmicas ACDB, tanto os lados quanto os ângulos opostos são iguais entre si (p. 124). “... digo que tanto os lados quanto os ângulos opostos do paralelogramo ACDB são iguais entre si...”
Paralelogramo ABCDparalelogramo retangular ou retângulo é dito ser contido pelas duas retas que contêm o ângulo reto
paralelogramo equilátero é tido por Euclides como uma figura quadrilátera que tem os quatro lados com a mesma medida
oblongo é retangular e não é equilátera
losango é equilátera e não é retangular
quadrado é aquela que é tanto equilátera quanto retangular
trapézios são as figuras quadriláteras além dessas

Em resumo Euclides define os quadriláteros da seguinte forma:

Quadriláteros Notáveis de Euclides.

No século XVIII, momento da Revolução Francesa (1789) e período do apogeu das ideias iluministas podemos destacar Legendre como um matemático, que como resposta a sua inquietação com relação à necessidade de maior rigor matemático, revive em sua obra intitulada por “Elements de geométrie”, a qualidade intelectual de Euclides, Legendre nesta obra, especificamente no capítulo, Princípios, livro I, afirma que os polígonos de quatro lados são chamados de quadriláteros e entre os quadriláteros, os que mais se distingue são:

o paralelogramo ou rombo, que tem os lados paralelos (p.25).
o retângulo, que tem os ângulos retos e não tem os lados iguais (p. 25).
o losango, que tem os lados iguais, mas os ângulos não (necessariamente) retos (p. 25).
o quadrado, que tem os lados iguais e os ângulos retos (p. 25).
o trapézio, que só têm dois lados paralelos (p. 25).

Em resumo Legendre define os quadriláteros da seguinte forma: (figura 3)

Quadriláteros Notáveis de Legendre

Em seu livro: Geometria Elementar, primeira edição em 1971. Edwin M. Hemmerling, define os quadriláteros da seguinte maneira:

Quadriláteros: um polígono é um quadrilátero quando tem quatro lados (p. 205).
Trapézio: um quadrilátero é um trapézio se, e somente se ele tiver um, e apenas um par de lados paralelos. Os lados paralelos são as bases do trapézio. Os lados não paralelos são simplesmente lados (p. 207).
Trapézio isósceles: é aquele em que os lados não adjacentes são congruentes. Um par de ângulos que compartilham uma mesma base são chamados ângulos da base (p. 207).
Paralelogramo: um quadrilátero é um paralelogramo se, e somente se, os pares de lados opostos são paralelos. Qualquer lado pode ser considerado base (p. 208).
Losango: é um paralelogramo equilátero (p. 208).
Retângulo: é um paralelogramo que tem um ângulo reto. Um retângulo é quadrado se, e somente se, tem os quatro lados congruentes. Portanto é um retângulo equilátero (p. 208).

Em resumo Hemmerling define os quadriláteros da seguinte forma: (figura 4)

Quadriláteros Notáveis de Hemmerling

Geometria Euclidiana Plana de João Lucas Marques Barbosa

O livro “Geometria Euclidiana Plana” de João Lucas Marques Barbosa é um dos mais vendidos da Sociedade Brasileira de Matemática a cada ano, desde 1985. É tido como o livro que aborda a geometria axiomática de forma mais acessível para um educando iniciante nos estudos da Geometria Plana Euclidiana. Atualmente é o livro adotado pela Universidade Federal de Pernambuco para a formação de professores de Matemática na cadeira de Geometria Plana. Dessa forma, foi escolhido para a análise das definições dos quadriláteros. As definições seguintes foram adotadas por João Lucas neste livro:

Um paralelogramo é um quadrilátero cujos lados opostos são paralelos (p. 91).
Um retângulo é um quadrilátero que tem todos os seus ângulos, retos (p. 98).
Um losango (também denominado rombo) é um paralelogramo que tem todos os seus lados congruentes (p. 98).
Um quadrado é um retângulo que também é um losango (p. 98).
Um trapézio é um quadrilátero em que dois lados opostos são paralelos. Os lados paralelos de um trapézio são chamados bases e os outros dois são denominados de laterais (p. 98).

Em resumo João Lucas M.B. classifica os quadriláteros conforme exposto figura 5.

Quadriláteros Notáveis de João Lucas M.B.

Note que todos estes matemáticos consideram o conjunto dos quadriláteros como uma bipartição por disjunção, ou seja, não existem paralelogramos que são trapézios e vice – versa. Isto não anula a existência de estudos e literaturas que discutam a possibilidade de o conjunto dos paralelogramos ser um subconjunto do conjunto dos trapézios. É o caso dos estudos dos matemáticos: Guy Laville; Fritz Reinhardt et Heinrich Soeder em seu Atlas des Mathématiques; Vicenzo Bongiovanni na Revista do Professor de Matemática, Nª 72 e José Adelino Serrasqueiro no seu Tratado de Geometria Elementar.

Ver também

Referências

↑ Frank Ayres, Robert E. Moyer. Teoria E Prob. de Trigonometria (em português) Bookman, 2003. p. 185.
↑ a b c Dolce, O. (2013). Fundamentos de Matemática Elementar 9 ed. : Atual. ISBN 9788535716863
↑ «A soma dos ângulos internos de um quadrilátero convexo - Alunos Online». Alunos Online. Consultado em 22 de novembro de 2016
↑ Legendre, Adrien-Marie (2009). Elementos de Geometria. ISBN 978-85-61545-03-1
↑ castellanos, José Hernan Perez (1971). Geometría Elemental.
↑ Barbosa, João Lucas Marques (2006). Geometria Euclidiana Plana. ISBN 85-85818-02-6
↑ Laville, Guy. Géométrie pour le capes et l’agrégation. ellipses: ellipses – Edition marketing S. A., 1998, p. 199 e 212.
↑ Reinhardt, Fritz; SOEDER, Heinrich. Atlas des mathématiques. Paris: Librairie Générale Française, 1997, p. 162 – 163.
↑ Bongiovanni, Vicenzo. As diferentes definições dos quadriláteros notáveis. Revista do Professor de Matemática, PUC - São Paulo, n. 55.
↑ Serrasqueiro, José Adelino. Tratado de geometria elementar, composto segundo o programa oficial para o ensino desta ciência nos liceus. Coimbra, Livraria central de J. Diogo Pires, sucessoras, 1926, Livro quarto, cap. 1, p. 97 – 105.

v d e Polígonos
Convexos	Triângulo · Quadrilátero · Heptágono · Octógono · Eneágono · Heptadecágono · Octodecágono · Hendecoságono · Docoságono · Pentacoságono · Triacontágono · Tetracontágono · Quiliágono · 65537-gono
Estrelas	Pentagrama · Hexagrama · Octograma

Controle de autoridade	: Q36810 AAT: 300158250