Círculo

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Abril de 2017)

Círculo
Um círculo circunfêrencia C diâmetro D raio R centro ou origem O

Na geometria, um círculo é o conjunto dos pontos internos de uma circunferência. Por vezes, também se chama círculo o conjunto de pontos cuja distância ao centro O {\displaystyle O} $O$ é menor ou igual a um dado valor (ao qual chamamos raio r {\displaystyle r} $r$ ). A área A {\displaystyle A} $A$ de um círculo pode ser expressa matematicamente por:

A = π × r 2 {\displaystyle A=\pi \times r^{2}}

A=\pi \times r^{2}

onde r {\displaystyle r} $r$ é o raio da circunferência e π {\displaystyle \pi } $\pi$ (Pi) uma constante.

O círculo é conhecido desde antes do início da história registrada. Os círculos naturais são comuns, como a lua cheia ou uma fatia de fruta redonda. O círculo é a base da roda, que, com invenções relacionadas, como as engrenagens, torna possível grande parte do maquinário moderno. Na matemática, o estudo do círculo ajudou a inspirar o desenvolvimento da geometria, da astronomia e do cálculo.

Etimologia

A palavra círculo deriva do grego κίρκος/κύκλος (kirkos/kuklos), que é uma metátese do grego homérico κρίκος (krikos), que significa "aro" ou "anel". As origens das palavras circo e circuito estão intimamente relacionadas.

Terminologia

Anel: um objeto em forma de anel, a região delimitada por dois círculos concêntricos.
Arco: qualquer parte conectada de um círculo. A especificação de dois pontos finais de um arco e de um centro permite a criação de dois arcos que, juntos, formam um círculo completo.
Centro: o ponto equidistante de todos os pontos do círculo.
Corda: um segmento de linha cujos pontos finais estão no círculo, dividindo assim um círculo em dois segmentos.
Circunferência: lugar geométrico dos pontos de um plano que equidistam (raio r {\displaystyle r} $r$ ) de um ponto fixo (centro O {\displaystyle O} $O$ )
Diâmetro: um segmento de linha cujos pontos finais estão sobre a circunferência e que passa pelo centro; ou o comprimento desse segmento de linha. Essa é a maior distância entre dois pontos quaisquer do círculo. É um caso especial de uma corda, ou seja, a corda mais longa para uma determinada circunferência, e seu comprimento é duas vezes o comprimento de um raio.
Disco: a região do plano delimitada por um círculo. Algumas definições determinam que um círculo é apenas o limite do disco, enquanto outras afirmam que "círculo" e "disco" podem ser usados de forma intercambiável.
Lente: a região comum a (a interseção de) dois discos sobrepostos.
Raio: segmento de reta que une o centro de um círculo a qualquer ponto do próprio círculo; ou o comprimento desse segmento, que é a metade (do comprimento) de um diâmetro. Normalmente, o raio é denotado por r {\displaystyle r} $r$ e deve ser um número positivo. Um círculo com r = 0 {\displaystyle r=0} $r=0$ é um caso degenerado que consiste em um único ponto.

Corda, secante, tangente, raio e diâmetro.

Setor: uma região limitada por dois raios de igual comprimento com um centro comum e um dos dois arcos possíveis, determinados por esse centro e pelos pontos finais dos raios.

Segmento: uma região delimitada por uma corda e um dos arcos que conectam os pontos finais da corda. O comprimento da corda impõe um limite inferior ao diâmetro dos possíveis arcos. Às vezes, o termo segmento é usado apenas para regiões que não contêm o centro do círculo ao qual o arco pertence.
Secante: uma corda estendida, uma linha reta coplanar, que intercepta um círculo em dois pontos.
Semicírculo: um dos dois arcos possíveis determinados pelos pontos finais de um diâmetro, tendo seu ponto médio como centro. No uso comum não técnico, pode significar o interior da região bidimensional delimitada por um diâmetro e um de seus arcos, que é tecnicamente chamado de semidisco. Um meio disco é um caso especial de um segmento, ou seja, o maior deles.
Tangente: uma linha reta coplanar que tem um único ponto em comum com um círculo ("toca o círculo nesse ponto").

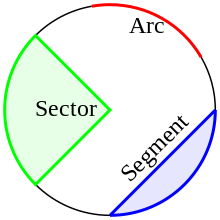Arco, setor e segmento.

Todas as regiões especificadas podem ser consideradas como abertas, ou seja, não contendo seus limites, ou como fechadas, incluindo seus respectivos limites.

História

Os povos pré-históricos fizeram círculos de pedra e círculos de madeira, e elementos circulares são comuns em petróglifos e pinturas rupestres. Os artefatos pré-históricos em forma de disco incluem o Disco de Nebra e os discos de jade chamados Bi.

O papiro egípcio de Rhind, datado de 1700 a.C., apresenta um método para encontrar a área de um círculo. O resultado corresponde a 25681 (3,16049...) como um valor aproximado de π {\displaystyle \pi } $\pi$ .

O Livro 3 de Os Elementos de Euclides trata das propriedades dos círculos. A definição de círculo de Euclides é a seguinte:

Uma circunferência é uma figura plana delimitada por uma linha curva e tal que todas as linhas retas traçadas de um certo ponto dentro dela até a linha de delimitação são iguais. A linha de delimitação é chamada de circunferência e o ponto, de centro.— Euclides, Os Elementos, Livro I

Na Sétima Carta de Platão, há uma definição e explicação detalhadas do círculo. Platão explica o círculo perfeito e como ele é diferente de qualquer desenho, palavra, definição ou explicação. A ciência primitiva, particularmente a geometria, a astrologia e a astronomia, estava ligada ao divino para a maioria dos estudiosos medievais, e muitos acreditavam que havia algo intrinsecamente "divino" ou "perfeito" que poderia ser encontrado nos círculos.

Em 1880 d.C., Ferdinand von Lindemann provou que π {\displaystyle \pi } $\pi$ é transcendente, demonstrando que o problema milenar da quadratura do círculo não pode ser realizado com régua e compasso.

Com o advento da arte abstrata no início do século XX, os objetos geométricos se tornaram um tema artístico por si só. Wassily Kandinsky, em particular, usava círculos com frequência como um elemento de suas composições.

Simbolismo e uso religioso

O compasso neste manuscrito do século XIII é um símbolo do ato de criação de Deus. Observe também a forma circular da auréola.

Desde os tempos das primeiras civilizações conhecidas - como os assírios e os egípcios antigos, os do Vale do Indo e ao longo do Rio Amarelo na China, e as civilizações ocidentais da Grécia e Roma antigas durante a Antiguidade Clássica - o círculo tem sido usado direta ou indiretamente na arte visual para transmitir a mensagem do artista e expressar determinadas ideias. No entanto, as diferenças de visão de mundo (crenças e cultura) tiveram um grande impacto sobre as percepções dos artistas. Enquanto alguns enfatizaram o perímetro do círculo para demonstrar sua manifestação democrática, outros se concentraram em seu centro para simbolizar o conceito de unidade cósmica. Nas doutrinas místicas, o círculo simboliza principalmente a natureza infinita e cíclica da existência, mas nas tradições religiosas ele representa corpos celestes e espíritos divinos.

O círculo significa muitos conceitos sagrados e espirituais, incluindo unidade, infinidade, totalidade, universo, divindade, equilíbrio, estabilidade e perfeição, entre outros. Tais conceitos foram transmitidos em culturas do mundo todo por meio do uso de símbolos, por exemplo, uma bússola, um halo, a vesica piscis e seus derivados (peixe, olho, aureola, mandorla etc.), o ouroboros, a roda do darma, um arco-íris, mandalas, rosáceas etc. Os círculos mágicos fazem parte de algumas tradições do esoterismo ocidental.

1ª Demonstração

Considere-se uma sucessão de polígonos regulares inscritos na circunferência. A área de cada um desses polígonos é dada por S = p ⋅ a {\displaystyle S=p\cdot a} $S=p\cdot a$ , onde p {\displaystyle p} $p$ é o semiperímetro do polígono e a {\displaystyle a} $a$ é o seu apótema. À medida que o número de lados do polígono aumenta, p {\displaystyle p} $p$ converge para a metade do comprimento da circunferência ( π R {\displaystyle \pi R} $\pi R$ ) e a {\displaystyle a} $a$ converge para o raio ( R {\displaystyle R} $R$ ). Assim S {\displaystyle S} $S$ converge para π R ⋅ R = π R 2 {\displaystyle \pi R\cdot R=\pi R^{2}} $\pi R\cdot R=\pi R^{2}$ . Por outro lado, à medida que o número de lados do polígono cresce, a sua área converge para a área do círculo. Conclui-se assim que a área do círculo é π R 2 {\displaystyle \pi R^{2}} $\pi R^{2}$ .

2ª Demonstração

Seja f uma semicircunferência tal que:

f ( x ) = R 2 − x 2 {\displaystyle f(x)={\sqrt {R^{2}-x^{2}}}}

f(x)={\sqrt {R^{2}-x^{2}}}

Para calcular a área de um círculo, basta que calculemos a área abaixo do gráfico de uma semicircunferência e dobremo-la. Portanto, basta calcular a integral definida:

F ( x ) = ∫ a x f ( t 2 ) d t {\displaystyle F(x)=\int _{a}^{x}f(t^{2})dt}

F(x)=\int _{a}^{x}f(t^{2})dt

uma circunferência em R 2 : {\displaystyle \mathbb {R} ^{2}:} $\mathbb {R} ^{2}:$

x 2 + y 2 = R 2 {\displaystyle x^{2}+y^{2}=R^{2}}

x^{2}+y^{2}=R^{2}

Geometria analítica

Em geometria analítica é possível descrever o circulo como o lugar geométrico de todos os pontos que estão a uma distância menor ou igual a um valor r {\displaystyle r} $r$ (chamado de raio) de um ponto O {\displaystyle O} $O$ fixo (chamado de centro ou origem).

Numericamente pode-se descrever o circulo pela seguinte equação:

( x − x o ) 2 + ( y − y o ) 2 ≤ r 2 {\displaystyle \left(x-x_{o}\right)^{2}+\left(y-y_{o}\right)^{2}\leq r^{2}} $\left(x-x_{o}\right)^{2}+\left(y-y_{o}\right)^{2}\leq r^{2}$

Onde x c {\displaystyle x_{c}} $x_{c}$ e y c {\displaystyle y_{c}} $y_{c}$ são as coordenadas do centro O {\displaystyle O} $O$ e r {\displaystyle r} $r$ o raio do circulo.

Resultados analíticos

Circunferência

A razão entre a circunferência de um círculo e seu diâmetro é π {\displaystyle \pi } $\pi$ (pi), uma constante irracional aproximadamente igual a 3,141592654. Assim, a circunferência O {\displaystyle O} $O$ está relacionada ao raio r {\displaystyle r} $r$ e ao diâmetro d por:

O = 2 π r = π d . {\displaystyle O=2\pi r=\pi d.}

O=2\pi r=\pi d.

Área

Conforme demonstrado por Arquimedes, em sua obra A Medida do Círculo, a área delimitada por um círculo é igual à de um triângulo cuja base tem o comprimento da circunferência do círculo e cuja altura é igual ao raio do círculo, o que resulta em π {\displaystyle \pi } $\pi$ multiplicado pelo raio ao quadrado:

A r e a = π r 2 . {\displaystyle \mathrm {Area} =\pi r^{2}.}

\mathrm {Area} =\pi r^{2}.

De forma equivalente, denotando o diâmetro por d, A r e a = π d 2 4 ≈ 0.7854 d 2 , {\displaystyle \mathrm {Area} ={\frac {\pi d^{2}}{4}}\approx 0.7854d^{2},}

\mathrm {Area} ={\frac {\pi d^{2}}{4}}\approx 0.7854d^{2},

ou seja, aproximadamente 79% do quadrado circunscrito (cujo lado é de comprimento d).

A circunferência é a curva plana que abrange a área máxima para um determinado comprimento de arco. Isso relaciona o círculo a um problema no cálculo de variações, a saber, a desigualdade isoperimétrica.

Equações

Coordenadas cartesianas

Círculo de raio r = 1, centro (a, b) = (1,2, -0,5) Equação de um círculo

Em um sistema de coordenadas cartesianas x , y {\displaystyle x,y} $x,y$ , a circunferência com coordenadas de centro ( a , b {\displaystyle a,b} $a,b$ ) e raio r {\displaystyle r} $r$ é o conjunto de todos os pontos ( x , y {\displaystyle x,y} $x,y$ ) de modo que

( x − a ) 2 + ( y − b ) 2 = r 2 . {\displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}.}

(x-a)^{2}+(y-b)^{2}=r^{2}.

Essa equação, conhecida como equação da circunferência, decorre do teorema de Pitágoras aplicado a qualquer ponto da circunferência: conforme mostrado no diagrama ao lado, o raio é a hipotenusa de um triângulo retângulo cujos outros lados têm comprimento | x − a | {\displaystyle |x-a|}

|x-a|

e | y − b | {\displaystyle |y-b|}

|y-b|

. Se o círculo estiver centrado na origem ( 0 , 0 {\displaystyle 0,0}

0,0

), então a equação se simplifica para x 2 + y 2 = r 2 . {\displaystyle x^{2}+y^{2}=r^{2}.}

x^{2}+y^{2}=r^{2}.

Forma paramétrica A equação pode ser escrita na forma paramétrica usando as funções trigonométricas seno e cosseno como x = a + r cos ⁡ t , y = b + r sen ⁡ t , {\displaystyle {\begin{aligned}x&=a+r\,\cos t,\\y&=b+r\,\operatorname {sen} t,\end{aligned}}}

{\begin{aligned}x&=a+r\,\cos t,\\y&=b+r\,\operatorname {sen} t,\end{aligned}}

em que t é uma variável paramétrica no intervalo de 0 {\displaystyle 0}

0

a 2 π {\displaystyle 2\pi }

2\pi

, interpretada geometricamente como o ângulo que o raio de ( a , b {\displaystyle a,b}

a,b

) a ( x , y {\displaystyle x,y}

x,y

) faz com o eixo x {\displaystyle x}

x

positivo.

Uma parametrização alternativa do círculo é

x = a + r 1 − t 2 1 + t 2 , y = b + r 2 t 1 + t 2 . {\displaystyle {\begin{aligned}x&=a+r{\frac {1-t^{2}}{1+t^{2}}},\\y&=b+r{\frac {2t}{1+t^{2}}}.\end{aligned}}}

{\begin{aligned}x&=a+r{\frac {1-t^{2}}{1+t^{2}}},\\y&=b+r{\frac {2t}{1+t^{2}}}.\end{aligned}}

Nessa parametrização, a proporção de t {\displaystyle t}

t

para r {\displaystyle r}

r

pode ser interpretada geometricamente como a projeção estereográfica da linha que passa pelo centro paralelamente ao eixo x {\displaystyle x}

x

(consulte substituição de meio-ângulo tangente). No entanto, essa parametrização funciona somente se t {\displaystyle t}

t

for feito para abranger não somente todos os reais, mas também um ponto no infinito; caso contrário, o ponto mais à esquerda do círculo seria omitido. Determinação por três pontos

A equação da circunferência determinada por três pontos ( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) {\displaystyle (x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})} $(x_{1},y_{1}),(x_{2},y_{2}),(x_{3},y_{3})$ não em uma linha é obtida por uma conversão da forma de 3 pontos de uma equação de círculo:

( x − x 1 ) ( x − x 2 ) + ( y − y 1 ) ( y − y 2 ) ( y − y 1 ) ( x − x 2 ) − ( y − y 2 ) ( x − x 1 ) = ( x 3 − x 1 ) ( x 3 − x 2 ) + ( y 3 − y 1 ) ( y 3 − y 2 ) ( y 3 − y 1 ) ( x 3 − x 2 ) − ( y 3 − y 2 ) ( x 3 − x 1 ) . {\displaystyle {\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.}

{\frac {({\color {green}x}-x_{1})({\color {green}x}-x_{2})+({\color {red}y}-y_{1})({\color {red}y}-y_{2})}{({\color {red}y}-y_{1})({\color {green}x}-x_{2})-({\color {red}y}-y_{2})({\color {green}x}-x_{1})}}={\frac {(x_{3}-x_{1})(x_{3}-x_{2})+(y_{3}-y_{1})(y_{3}-y_{2})}{(y_{3}-y_{1})(x_{3}-x_{2})-(y_{3}-y_{2})(x_{3}-x_{1})}}.

Forma homogênea Em coordenadas homogêneas, cada seção cônica com a equação de um círculo tem a forma x 2 + y 2 − 2 a x z − 2 b y z + c z 2 = 0. {\displaystyle x^{2}+y^{2}-2axz-2byz+cz^{2}=0.}

x^{2}+y^{2}-2axz-2byz+cz^{2}=0.

Pode-se provar que uma seção cônica é um círculo exatamente quando ela contém (quando estendida ao plano projetivo complexo) os pontos I ( 1 : i : 0 ) {\displaystyle I(1:i:0)}

I(1:i:0)

e J ( 1 : − i : 0 ) {\displaystyle J(1:-i:0)}

J(1:-i:0)

. Esses pontos são chamados de pontos circulares no infinito. Coordenadas polares

Em coordenadas polares, a equação de um círculo é

r 2 − 2 r r 0 cos ⁡ ( θ − ϕ ) + r 0 2 = a 2 , {\displaystyle r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2},}

r^{2}-2rr_{0}\cos(\theta -\phi )+r_{0}^{2}=a^{2},

onde a {\displaystyle a}

a

é o raio do círculo, ( r , θ ) {\displaystyle (r,\theta )}

(r,\theta )

são as coordenadas polares de um ponto genérico no círculo, e ( r 0 , ϕ ) {\displaystyle (r_{0},\phi )}

(r_{0},\phi )

as coordenadas polares do centro da circunferência (ou seja, r 0 {\displaystyle r_{0}}

r_{0}

é a distância da origem até o centro da circunferência e ϕ {\displaystyle \phi }

\phi

é o ângulo anti-horário do eixo x {\displaystyle x}

x

positivo até a linha que liga a origem ao centro da circunferência). Para um círculo centrado na origem, ou seja, r 0 = 0 {\displaystyle r_{0}=0}

r_{0}=0

, isso se reduz a r = a {\displaystyle r=a}

r=a

. Quando r 0 = a {\displaystyle r_{0}=a}

r_{0}=a

, ou quando a origem está no círculo, a equação se torna r = 2 a cos ⁡ ( θ − ϕ ) . {\displaystyle r=2a\cos(\theta -\phi ).}

r=2a\cos(\theta -\phi ).

No caso geral, a equação pode ser resolvida para r {\displaystyle r}

r

, dando r = r 0 cos ⁡ ( θ − ϕ ) ± a 2 − r 0 2 sin 2 ⁡ ( θ − ϕ ) . {\displaystyle r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\theta -\phi )}}.}

r=r_{0}\cos(\theta -\phi )\pm {\sqrt {a^{2}-r_{0}^{2}\sin ^{2}(\theta -\phi )}}.

Sem o sinal ± {\displaystyle \pm }

\pm

, a equação descreveria, em alguns casos, apenas metade de um círculo. Plano complexo

No plano complexo, um círculo com centro em o {\displaystyle o} $o$ e raio r {\displaystyle r} $r$ tem a equação

| z − o | = r . {\displaystyle |z-o|=r.}

|z-o|=r.

Na forma paramétrica, isso pode ser escrito como z = r e i t + o . {\displaystyle z=re^{it}+o.}

z=re^{it}+o.

A equação ligeiramente generalizada p z z ¯ + g z + g z ¯ = q {\displaystyle pz{\overline {z}}+gz+{\overline {gz}}=q}

pz{\overline {z}}+gz+{\overline {gz}}=q

para p {\displaystyle p}

p

, q {\displaystyle q}

q

reais e g {\displaystyle g}

g

complexo às vezes é chamado de círculo generalizado. Isso se torna a equação acima para um círculo com p = 1 , g = − o ¯ , q = r 2 − | o | 2 {\displaystyle p=1,\ g=-{\overline {o}},\ q=r^{2}-|o|^{2}}

p=1,\ g=-{\overline {o}},\ q=r^{2}-|o|^{2}

já que | z − o | 2 = z z ¯ − o ¯ z − c z ¯ + c o ¯ {\displaystyle |z-o|^{2}=z{\overline {z}}-{\overline {o}}z-c{\overline {z}}+c{\overline {o}}}

|z-o|^{2}=z{\overline {z}}-{\overline {o}}z-c{\overline {z}}+c{\overline {o}}

. Nem todos os círculos generalizados são de fato círculos: um círculo generalizado é um círculo (verdadeiro) ou uma linha.

Linhas tangentes

A linha tangente que passa por um ponto P {\displaystyle P} $P$ na circunferência é perpendicular ao diâmetro que passa por P {\displaystyle P} $P$ . Se P = ( x 1 , y 1 ) {\displaystyle P=(x_{1},y_{1})} $P=(x_{1},y_{1})$ e a circunferência tem centro ( a , b {\displaystyle a,b} $a,b$ ) e raio r {\displaystyle r} $r$ , então a linha tangente é perpendicular à linha de ( a , b {\displaystyle a,b} $a,b$ ) a ( x 1 , y 1 {\displaystyle x_{1},y_{1}} $x_{1},y_{1}$ ), de modo que tem a forma ( x 1 − a ) x + ( y 1 − b ) y = c {\displaystyle (x_{1}-a)x+(y_{1}-b)y=c} $(x_{1}-a)x+(y_{1}-b)y=c$ . A avaliação em ( x 1 , y 1 {\displaystyle x_{1},y_{1}} $x_{1},y_{1}$ ) determina o valor de c {\displaystyle c} $c$ , e o resultado é que a equação da tangente é

( x 1 − a ) x + ( y 1 − b ) y = ( x 1 − a ) x 1 + ( y 1 − b ) y 1 , {\displaystyle (x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1},} $(x_{1}-a)x+(y_{1}-b)y=(x_{1}-a)x_{1}+(y_{1}-b)y_{1},$

( x 1 − a ) ( x − a ) + ( y 1 − b ) ( y − b ) = r 2 . {\displaystyle (x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}.} $(x_{1}-a)(x-a)+(y_{1}-b)(y-b)=r^{2}.$

Se y 1 ≠ b {\displaystyle y_{1}\neq b} $y_{1}\neq b$ , então a inclinação dessa linha é

d y d x = − x 1 − a y 1 − b . {\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.} ${\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.$

Isso também pode ser encontrado usando a diferenciação implícita.

Quando o centro do círculo está na origem, a equação da reta tangente se torna

d y d x = − x 1 − a y 1 − b . {\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.} ${\frac {dy}{dx}}=-{\frac {x_{1}-a}{y_{1}-b}}.$

e sua inclinação é

d y d x = − x 1 y 1 . {\displaystyle {\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}.} ${\frac {dy}{dx}}=-{\frac {x_{1}}{y_{1}}}.$

Propriedades

O círculo é a forma com a maior área para um determinado comprimento de perímetro (consulte desigualdade isoperimétrica).
O círculo é uma forma altamente simétrica: cada linha que passa pelo centro forma uma linha de simetria de reflexão, e ele tem simetria rotacional em torno do centro para cada ângulo. Seu grupo de simetria é o grupo ortogonal O ( 2 , R ) {\displaystyle O(2,R)} $O(2,R)$ . O grupo de rotações sozinho é o grupo de círculos T {\displaystyle T} $T$ .
Todos os círculos são semelhantes:
- A circunferência e o raio de um círculo são proporcionais.
- A área delimitada e o quadrado de seu raio são proporcionais.
- As constantes de proporcionalidade são 2 π {\displaystyle 2\pi } $2\pi$ e π {\displaystyle \pi } $\pi$ , respectivamente.
O círculo centrado na origem com raio 1 é chamado de círculo unitário.
- Considerado como um círculo máximo da esfera unitária, ele se torna o círculo Riemanniano.
Através de quaisquer três pontos, nem todos na mesma linha, há um círculo único. Em coordenadas cartesianas, é possível fornecer fórmulas explícitas para as coordenadas do centro do círculo e do raio em termos das coordenadas dos três pontos dados. Consulte circunferência circunscrita.

Cordas

As cordas são equidistantes do centro de um círculo se e somente se tiverem o mesmo comprimento.
A bissetriz perpendicular de uma corda passa pelo centro de uma circunferência; as afirmações equivalentes decorrentes da exclusividade da bissetriz perpendicular são:
- Uma linha perpendicular ao centro de uma circunferência divide a corda.
- O segmento de reta que passa pelo centro e divide uma corda é perpendicular à corda.
Se um ângulo central e um ângulo inscrito em uma circunferência são subtendidos pela mesma corda e estão no mesmo lado da corda, então o ângulo central é o dobro do ângulo inscrito.
Se dois ângulos estiverem inscritos na mesma corda e no mesmo lado da corda, eles são iguais.
Se dois ângulos estiverem inscritos na mesma corda e em lados opostos da corda, eles serão suplementares.
- Em um quadrilátero cíclico, o ângulo externo é igual ao ângulo interno oposto.
Um ângulo inscrito subtendido por um diâmetro é um ângulo reto (consulte o teorema de Tales).
O diâmetro é a corda mais longa do círculo.
- Entre todos os círculos com uma corda A B {\displaystyle AB} $AB$ em comum, o círculo com raio mínimo é aquele com diâmetro A B {\displaystyle AB} $AB$ .
Se a interseção de duas cordas quaisquer divide uma corda em comprimentos a {\displaystyle a} $a$ e b {\displaystyle b} $b$ e divide a outra corda em comprimentos c {\displaystyle c} $c$ e d {\displaystyle d} $d$ , então a b = c d {\displaystyle ab=cd} $ab=cd$ .
Se a interseção de quaisquer duas cordas perpendiculares divide uma corda em comprimentos a e b e divide a outra corda em comprimentos c e d, então a 2 + b 2 + c 2 + d 2 {\displaystyle a^{2}+b^{2}+c^{2}+d^{2}} $a^{2}+b^{2}+c^{2}+d^{2}$ é igual ao quadrado do diâmetro.
A soma dos comprimentos ao quadrado de quaisquer duas cordas que se cruzam em ângulos retos em um determinado ponto é a mesma de quaisquer outras duas cordas perpendiculares que se cruzam no mesmo ponto e é dada por 8 r 2 − 4 p 2 {\displaystyle 8r^{2}-4p^{2}} $8r^{2}-4p^{2}$ , onde r {\displaystyle r} $r$ é o raio do círculo e p {\displaystyle p} $p$ é a distância do ponto central ao ponto de interseção.
A distância de um ponto da circunferência a uma determinada corda vezes o diâmetro da circunferência é igual ao produto das distâncias do ponto às extremidades da corda.:71

Tangente

Uma linha perpendicular a um raio que passa pelo ponto final do raio situado na circunferência é uma tangente à circunferência.
Uma linha perpendicular a uma tangente que passa pelo ponto de contato com um círculo passa pelo centro do círculo.
Sempre é possível traçar duas tangentes a uma circunferência a partir de qualquer ponto fora da circunferência, e essas tangentes são iguais em comprimento.
Se uma tangente em A {\displaystyle A} $A$ e uma tangente em B {\displaystyle B} $B$ se cruzam no ponto exterior P {\displaystyle P} $P$ , então, denotando o centro como O {\displaystyle O} $O$ , os ângulos ∠ B O A {\displaystyle \angle BOA} $\angle BOA$ e ∠ B P A {\displaystyle \angle BPA} $\angle BPA$ são suplementares.
Se A D {\displaystyle AD} $AD$ é tangente à circunferência em A {\displaystyle A} $A$ e se A Q {\displaystyle AQ} $AQ$ é uma corda da circunferência, então ∠ B O A = 1 2 a r c ( A Q ) {\displaystyle \angle BOA={\frac {1}{2}}arc(AQ)} $\angle BOA={\frac {1}{2}}arc(AQ)$ .

Teoremas

Teorema da secante-secante.

O teorema da corda afirma que, se duas cordas, C D {\displaystyle CD} $CD$ e E B {\displaystyle EB} $EB$ , se cruzam em A {\displaystyle A} $A$ , então A C × A D = A B × A E {\displaystyle AC\times AD=AB\times AE} $AC\times AD=AB\times AE$ .
Se duas secantes, A E {\displaystyle AE} $AE$ e A D {\displaystyle AD} $AD$ , também cortam o círculo em B {\displaystyle B} $B$ e C {\displaystyle C} $C$ , respectivamente, então A C × A D = A B × A E {\displaystyle AC\times AD=AB\times AE} $AC\times AD=AB\times AE$ (corolário do teorema da corda).
Uma tangente pode ser considerada um caso limite de uma secante cujas extremidades são coincidentes. Se uma tangente de um ponto externo A {\displaystyle A} $A$ encontra o círculo em F {\displaystyle F} $F$ e uma secante do ponto externo A {\displaystyle A} $A$ encontra o círculo em C {\displaystyle C} $C$ e D {\displaystyle D} $D$ , respectivamente, então A F 2 = A C × A D {\displaystyle AF^{2}=AC\times AD} $AF^{2}=AC\times AD$ (teorema da tangente-secante).
O ângulo entre uma corda e a tangente em um de seus pontos finais é igual à metade do ângulo subtendido no centro da circunferência, no lado oposto da corda (ângulo da corda tangente).
Se o ângulo subtendido pela corda no centro for 90°, então ℓ = r 2 {\displaystyle \ell =r{\sqrt {2}}} $\ell =r{\sqrt {2}}$ , em que ℓ {\displaystyle \ell } $\ell$ é o comprimento da corda e r {\displaystyle r} $r$ é o raio da circunferência.
Se duas secantes estiverem inscritas na circunferência, conforme mostrado à direita, a medida do ângulo A {\displaystyle A} $A$ será igual à metade da diferença das medidas dos arcos circunscritos ( D E ⌢ {\displaystyle {\displaystyle {\overset {\frown }{DE}}}} ${\displaystyle {\overset {\frown }{DE}}}$ e B C ⌢ {\displaystyle {\displaystyle {\overset {\frown }{BC}}}} ${\displaystyle {\overset {\frown }{BC}}}$ ). Isto é, 2 ∠ C A B = ∠ D O E − ∠ B O C {\displaystyle {\displaystyle 2\angle {CAB}=\angle {DOE}-\angle {BOC}}} ${\displaystyle 2\angle {CAB}=\angle {DOE}-\angle {BOC}}$ , onde O {\displaystyle O} $O$ é o centro do círculo (teorema da secante-secante).

Ângulos inscritos

Teorema do ângulo inscrito

Um ângulo inscrito (exemplos são os ângulos azul e verde na figura) é exatamente a metade do ângulo central correspondente (vermelho). Portanto, todos os ângulos inscritos que subtendem o mesmo arco (rosa) são iguais. Os ângulos inscritos no arco (marrom) são suplementares. Em particular, todo ângulo inscrito que subtende um diâmetro é um ângulo reto (já que o ângulo central é 180°).

Construções com bússola e régua

Há muitas construções de compasso e régua que resultam em círculos.

A mais simples e mais básica é a construção em que se dá o centro do círculo e um ponto no círculo. Coloque a perna fixa do compasso no ponto central, a perna móvel no ponto do círculo e gire o compasso.

Construção com um determinado diâmetro

Construa o ponto médio M {\displaystyle M} $M$ do diâmetro.
Construa o círculo com o centro M {\displaystyle M} $M$ passando por um dos pontos finais do diâmetro (ele também passará pelo outro ponto final).

Construa um círculo que passe pelos pontos A, B e C encontrando as bissetrizes perpendiculares (vermelho) dos lados do triângulo (azul). Apenas duas das três bissetrizes são necessárias para encontrar o centro.

Construção através de três pontos não colineares

Nomeie os pontos P {\displaystyle P} $P$ , Q {\displaystyle Q} $Q$ e R {\displaystyle R} $R$ .
Construa a bissetriz perpendicular do segmento P Q ¯ {\displaystyle {\overline {PQ}}} ${\overline {PQ}}$ .
Construa a bissetriz perpendicular do segmento P R ¯ {\displaystyle {\overline {PR}}} ${\overline {PR}}$ .
Nomeie o ponto de interseção dessas duas bissetrizes perpendiculares como M {\displaystyle M} $M$ . (Elas se encontram porque os pontos não são colineares).
Construa o círculo com centro M {\displaystyle M} $M$ passando por um dos pontos P {\displaystyle P} $P$ , Q {\displaystyle Q} $Q$ ou R {\displaystyle R} $R$ (ele também passará pelos outros dois pontos).

Círculo de Apolônio

Definição de Apolônio de um círculo: d 1 / d 2 {\displaystyle d_{1}/d_{2}}

d_{1}/d_{2}

constante

Apolônio de Perga mostrou que um círculo também pode ser definido como o conjunto de pontos em um plano com uma razão constante (diferente de 1) de distâncias para dois focos fixos, A {\displaystyle A} $A$ e B {\displaystyle B} $B$ . O conjunto de pontos em que as distâncias são iguais é a bissetriz perpendicular do segmento A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ , uma linha. Às vezes, diz-se que esse círculo é desenhado em torno de dois pontos.

A prova está dividida em duas partes. Primeiro, é preciso provar que, dados dois focos A {\displaystyle A} $A$ e B {\displaystyle B} $B$ e uma razão de distâncias, qualquer ponto P {\displaystyle P} $P$ que satisfaça a razão de distâncias deve cair em um círculo específico. Seja C {\displaystyle C} $C$ outro ponto, também satisfazendo a razão e situado no segmento A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ . Pelo teorema da bissetriz do ângulo, o segmento de reta P C ¯ {\displaystyle {\overline {PC}}} ${\overline {PC}}$ dividirá o ângulo interno A P B ^ {\displaystyle {\widehat {APB}}} ${\widehat {APB}}$ , já que os segmentos são semelhantes:

A P B P = A C B C . {\displaystyle {\frac {AP}{BP}}={\frac {AC}{BC}}.} ${\frac {AP}{BP}}={\frac {AC}{BC}}.$

Da mesma forma, um segmento de reta P D ¯ {\displaystyle {\overline {PD}}} ${\overline {PD}}$ que passa por algum ponto D {\displaystyle D} $D$ em A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ estendido divide o ângulo externo correspondente BPQ, onde Q está em AP estendido. Como os ângulos interno e externo somam 180 graus, o ângulo C P D ^ {\displaystyle {\widehat {CPD}}} ${\widehat {CPD}}$ é exatamente 90 graus, ou seja, um ângulo reto. O conjunto de pontos P {\displaystyle P} $P$ em que o ângulo C P D ^ {\displaystyle {\widehat {CPD}}} ${\widehat {CPD}}$ é um ângulo reto forma um círculo, do qual C D ¯ {\displaystyle {\overline {CD}}} ${\overline {CD}}$ é o diâmetro.

Em segundo lugar, consulte:15 para uma prova de que todos os pontos do círculo indicado satisfazem a proporção dada.

Razões cruzadas

Uma propriedade dos círculos intimamente relacionada envolve a geometria da razão cruzada de pontos no plano complexo. Se A {\displaystyle A} $A$ , B {\displaystyle B} $B$ e C {\displaystyle C} $C$ forem como acima, então o círculo de Apolônio para esses três pontos é o conjunto de pontos P {\displaystyle P} $P$ para os quais o valor absoluto da razão cruzada é igual a um:

| | = 1. {\displaystyle {\bigl |}{\bigr |}=1.} ${\bigl |}{\bigr |}=1.$

Em outras palavras, P {\displaystyle P} $P$ é um ponto no círculo de Apolônio se e somente se a relação cruzada {\displaystyle } $\text{[math]}$ estiver no círculo unitário no plano complexo.

Círculos generalizados

Veja também: Círculo generalizado

Se M {\displaystyle M} $M$ for o ponto médio do segmento A B ¯ {\displaystyle {\overline {AB}}} ${\overline {AB}}$ , então o conjunto de pontos P {\displaystyle P} $P$ que satisfazem a condição de Apolônio

| A P | | B P | = | A C | | B C | {\displaystyle {\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}}

{\frac {|AP|}{|BP|}}={\frac {|AC|}{|BC|}}

não é um círculo, mas sim uma linha.

Assim, se A {\displaystyle A} $A$ , B {\displaystyle B} $B$ e C {\displaystyle C} $C$ são pontos distintos no plano, então o local dos pontos P {\displaystyle P} $P$ que satisfazem a equação acima é chamado de "círculo generalizado". Ele pode ser um círculo verdadeiro ou uma linha. Nesse sentido, uma linha é um círculo generalizado de raio infinito.

Inscrição em ou circunscrição sobre outras figuras

Em todo triângulo, um único círculo, chamado de círculo inscrito, pode ser inscrito de modo que seja tangente a cada um dos três lados do triângulo.

Em todo triângulo, um único círculo, chamado de circunferência circunscrita, pode ser circunscrito de modo que passe por cada um dos três vértices do triângulo.

Um polígono tangencial, como um quadrilátero tangencial, é qualquer polígono convexo no qual pode ser inscrita uma circunferência tangente a cada lado do polígono. Todo polígono regular e todo triângulo é um polígono tangencial.

Um polígono cíclico é qualquer polígono convexo em torno do qual um círculo pode ser circunscrito, passando por cada vértice. Um exemplo bem estudado é o quadrilátero cíclico. Todo polígono regular e todo triângulo é um polígono cíclico. Um polígono que é cíclico e tangencial é chamado de polígono bicêntrico.

Uma hipocicloide é uma curva que é inscrita em um determinado círculo, traçando um ponto fixo em um círculo menor que rola dentro do círculo dado e é tangente a ele.

Caso limite de outras figuras

O círculo pode ser visto como um caso limite de várias outras figuras:

A série de polígonos regulares com n {\displaystyle n} $n$ lados tem o círculo como seu limite à medida que n {\displaystyle n} $n$ se aproxima do infinito. Esse fato foi aplicado por Arquimedes para aproximar π {\displaystyle \pi } $\pi$ .
Uma oval cartesiana é um conjunto de pontos em que a soma ponderada das distâncias de qualquer um de seus pontos a dois pontos fixos (focos) é uma constante. Uma elipse é o caso em que os pesos são iguais. Um círculo é uma elipse com excentricidade zero, o que significa que os dois focos coincidem um com o outro como centro do círculo. Um círculo também é um caso especial diferente de uma oval cartesiana em que um dos pesos é zero.
Uma superelipse tem uma equação do tipo | x a | n + | y b | n = 1 {\displaystyle \left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1} $\left|{\frac {x}{a}}\right|^{n}\!+\left|{\frac {y}{b}}\right|^{n}\!=1$ para a {\displaystyle a} $a$ , b {\displaystyle b} $b$ e n {\displaystyle n} $n$ positivos, um supercírculo tem b = a {\displaystyle b=a} $b=a$ . Um círculo é o caso especial de um supercírculo no qual n = 2 {\displaystyle n=2} $n=2$ .
Uma oval de Cassini é um conjunto de pontos em que o produto das distâncias de qualquer um de seus pontos por dois pontos fixos é uma constante. Quando os dois pontos fixos coincidem, o resultado é um círculo.
Uma curva de largura constante é uma figura cuja largura, definida como a distância perpendicular entre duas linhas paralelas distintas, cada uma delas cruzando seu limite em um único ponto, é a mesma, independentemente da direção dessas duas linhas paralelas. O círculo é o exemplo mais simples desse tipo de figura.

Locus de soma constante

Considere um conjunto finito de n {\displaystyle n} $n$ pontos no plano. O local dos pontos em que a soma dos quadrados das distâncias aos pontos dados é constante é um círculo, cujo centro está no centroide dos pontos dados. Uma generalização para potências maiores de distâncias é obtida se sob n {\displaystyle n} $n$ aponta os vértices do polígono regular P n {\displaystyle P_{n}} $P_{n}$ forem tomados. O local dos pontos em que a soma da 2 m {\displaystyle 2m} $2m$ -ésima potência das distâncias d i {\displaystyle d_{i}} $d_{i}$ aos vértices de um determinado polígono regular com circunferência de raio R {\displaystyle R} $R$ é constante é um círculo, se

∑ i = 1 n d i 2 m > n R 2 m , where m = 1 , 2 , … , n − 1 ; {\displaystyle \sum _{i=1}^{n}d_{i}^{2m}>nR^{2m},\quad {\text{ where }}~m=1,2,\dots ,n-1;} $\sum _{i=1}^{n}d_{i}^{2m}>nR^{2m},\quad {\text{ where }}~m=1,2,\dots ,n-1;$

cujo centro é o centroide do P n {\displaystyle P_{n}} $P_{n}$

No caso do triângulo equilátero, os loci das somas constantes da segunda e quarta potências são círculos, enquanto no caso do quadrado, os loci são círculos para as somas constantes da segunda, quarta e sexta potências. Para o pentágono regular, a soma constante das oitavas potências das distâncias será adicionada e assim por diante.

Elevação do círculo à quadratura

A quadratura do círculo é o problema, proposto por geômetras antigos, de construir um quadrado com a mesma área de um determinado círculo usando apenas um número finito de passos com compasso e régua.

Em 1882, foi provado que a tarefa era impossível, como consequência do teorema de Lindemann-Weierstrass, que prova que pi ( π {\displaystyle \pi } $\pi$ ) é um número transcendental, e não um número algébrico irracional; ou seja, não é a raiz de nenhum polinômio com coeficientes racionais. Apesar da impossibilidade, esse tópico continua a ser de interesse para os entusiastas da pseudomatemática.

Círculos com nomes especiais

Ver também

Referências

↑ MANFIO, Fernando. Fundamentos da Geometria. São Paulo: ICMC-USP. , v. 12, 2013.
↑ PAPA NETO, Angelo. Geometria Plana e Construções Geométricas. 2017
↑ krikos Arquivado em 2013-11-06 no Wayback Machine, Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
↑ Simek, Jan F.; Cressler, Alan; Herrmann, Nicholas P.; Sherwood, Sarah C. (1 de junho de 2013). «Sacred landscapes of the south-eastern USA: prehistoric rock and cave art in Tennessee». Antiquity (em inglês). 87 (336): 430–446. ISSN 0003-598X. doi:10.1017/S0003598X00049048
↑ Chronology for 30000 BC to 500 BC Arquivado em 2008-03-22 no Wayback Machine. History.mcs.st-andrews.ac.uk. Retrieved on 2012-05-03.
↑ Arthur Koestler, The Sleepwalkers: A History of Man's Changing Vision of the Universe (1959)
↑ Proclus, The Six Books of Proclus, the Platonic Successor, on the Theology of Plato Arquivado em 2017-01-23 no Wayback Machine Tr. Thomas Taylor (1816) Vol. 2, Ch. 2, "Of Plato"
↑ Squaring the circle Arquivado em 2008-06-24 no Wayback Machine. History.mcs.st-andrews.ac.uk. Retrieved on 2012-05-03.
↑ «Circles in a Circle». Philadelphia Museum of Art (em inglês). Consultado em 28 de dezembro de 2023
↑ Lesso, Rosie (15 de junho de 2022). «Why Did Wassily Kandinsky Paint Circles?». TheCollector (em inglês). Consultado em 28 de dezembro de 2023
↑ Abdullahi, Yahya (29 de outubro de 2019). «The Circle from East to West». In: Charnier, Jean-François. The Louvre Abu Dhabi: A World Vision of Art. Rizzoli International Publications, Incorporated. ISBN 9782370741004
↑ Mandarino, Denis - Desenho Geométrico, construções com régua e compasso. Ed. Plêiade, São Paulo: 2007., Cap.: Áreas.
↑ «Equações e Lugares Geométricos». Consultado em 11 de Junho de 2018
↑ Silva, Luiz. «Círculo e circunferência». Consultado em 11 de Junho de 2018
↑ Posamentier e Salkind, Challenging Problems in Geometry, Dover, 2a edição, 1996: pp. 104–105, #4–23.
↑ College Mathematics Journal 29(4), Setembro de 1998, p. 331, problema 635.
↑ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007.
↑ Harkness, James (1898). «Introduction to the theory of analytic functions». Nature. 59 (1530): 30. Bibcode:1899Natur..59..386B. doi:10.1038/059386a0. Cópia arquivada em 7 de outubro de 2008
↑ Ogilvy, C. Stanley, Excursions in Geometry, Dover, 1969, 14–17.
↑ Altshiller-Court, Nathan, College Geometry, Dover, 2007 (orig. 1952).
↑ Incircle – from Wolfram MathWorld Arquivado em 2012-01-21 no Wayback Machine. Mathworld.wolfram.com (2012-04-26). Acessado em 2012-05-03.
↑ Circumcircle – from Wolfram MathWorld Arquivado em 2012-01-20 no Wayback Machine. Mathworld.wolfram.com (2012-04-26). Acessado em 2012-05-03.
↑ Tangential Polygon – from Wolfram MathWorld Arquivado em 2013-09-03 no Wayback Machine. Mathworld.wolfram.com (2012-04-26). Acessado em 2012-05-03.
↑ Apostol, Tom; Mnatsakanian, Mamikon (2003). «Sums of squares of distances in m-space». American Mathematical Monthly. 110 (6): 516–526. doi:10.1080/00029890.2003.11919989
↑ Meskhishvili, Mamuka (2020). «Cyclic Averages of Regular Polygons and Platonic Solids». Communications in Mathematics and Applications. 11: 335–355. arXiv:2010.12340. doi:10.26713/cma.v11i3.1420 (inativo 31 de janeiro de 2024). Consultado em 17 de maio de 2021. Cópia arquivada em 22 de abril de 2021

Bibliografia

Braga, Theodoro - Desenho linear geométrico. Ed. Cone, São Paulo: 1997.
Carvalho, Benjamim - Desenho Geométrico. Ed. Ao Livro Técnico, São Paulo: 1982.
Giongo, Affonso Rocha - Curso de Desenho Geométrico. Ed. Nobel, São Paulo: 1954.
Marmo, Carlos - Desenho Geométrico. Ed. Scipione, São Paulo: 1995.
Putnoki, José Carlos - Elementos de geometria e desenho geométrico. Vol. 1 e 2. Ed. Scipione, São Paulo: 1990.

Ligações externas

Alfred North Whitehead: An Introduction to Mathematics. BiblioBazaar LLC 2009 (reprint), ISBN 9781103197842, pp. 121
George Wentworth: Junior High School Mathematics: Book III. BiblioBazaar LLC 2009 (reprint), ISBN 9781103152360, pp. 265
Robert Clarke James, Glenn James: Mathematics Dictionary. Springer 1992, ISBN 9780412990410, p. 255
«Construir objetos geometria analítica» (em inglês)