Teoria das filas

Aspeto mover para a barra lateral ocultar

Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Março de 2018)

Exemplo de fila de banco: Open House London, na Inglaterra

A teoria das filas é um ramo da probabilidade que estuda a formação de filas, através de análises matemáticas precisas e propriedades mensuráveis das filas. Ela provê modelos para demonstrar previamente o comportamento de um sistema que ofereça serviços cuja demanda cresce aleatoriamente, tornando possível dimensioná-lo de forma a satisfazer os clientes e ser viável economicamente para o provedor do serviço, evitando desperdícios e gargalos.

Definições

Um centro de serviço

Rede de filas - Conjunto de entidades interligadas que oferecem serviços (centros de serviço) e de usuários (clientes).
Centro de serviço - Representa os recursos do sistema, compreendendo um ou mais servidores e um conjunto de clientes que esperam pelo serviço.
Fila - Representa os clientes que estão esperando pelo serviço, juntamente com os que estão sendo atendidos pelos servidores.
Fila de espera - Somente os clientes que estão aguardando pelo serviço.

Sistema de filas

Uma fila ocorre sempre que a procura por um determinado serviço é maior que a capacidade do sistema de prover este serviço.

Um sistema de filas pode ser definido como clientes chegando, esperando pelo serviço (se não forem atendidos imediatamente) e saindo do sistema após terem sido atendidos. "Cliente", em teoria das filas, é um termo genérico, aplicando-se não somente a seres humanos. O conceito pode abranger, por exemplo, processos esperando para receber a CPU; pacotes que chegam a um roteador para serem encaminhados; pessoas esperando no caixa do supermercado, etc.

Aplicações

Existem diversas aplicações da teoria das filas, que podem ser encontradas na literatura de probabilidade, pesquisa operacional e engenharia industrial. Entre elas destacam-se:

Fluxo de tráfego (aviões, carros, pessoas, comunicações)
Escalonamento (pacientes em hospitais, programas em computadores)
Prestação de serviços (bancos, correios, lanchonetes)

Componentes de um sistema de filas

Um sistema de filas consiste no processo de chegada, da distribuição do tempo de serviço, do número de servidores, da capacidade do sistema, da população de usuários e da disciplina de atendimento.

Processo de chegada

O processo de chegada indica qual o padrão de chegada dos clientes no sistema. Apresenta comportamento estocástico, ou seja, as chegadas ocorrem no tempo e no espaço de acordo com as leis da probabilidade; assim, é preciso conhecer qual a distribuição de probabilidade que descreve os tempos entre as chegadas dos clientes.

A distribuição mais comum é a de Poisson, ou seja, os tempos entre as chegadas são exponencialmente distribuídos. Entre outras distribuições, estão a de Erlang, hiperexponencial e arbitrária.

Clientes podem chegar simultaneamente (chegada em batch). Se for possível, é necessário também saber a distribuição de probabilidade do tamanho do batch. A reação do cliente na fila pode variar. Ele pode esperar independentemente do tamanho da fila, também pode decidir não entrar no sistema caso a fila esteja muito grande (cliente decepcionado), ele pode esperar na fila mas depois de um tempo desistir e sair do sistema, e também pode mudar de uma fila para outra em sistemas com servidores paralelos.

O padrão de chegada de clientes em função do tempo pode ser permanente; nesse caso o padrão não muda no tempo, ou seja, a distribuição de probabilidade que descreve as chegadas é independente do tempo. Também pode não ser permanente, isto é, o padrão de chegada muda com o tempo. Por exemplo, a chegada de clientes diminui no horário de almoço.

Distribuição do tempo de serviço

Assim como no processo de chegada, também é necessário conhecer a distribuição de probabilidade do tempo de serviço, sendo válidas as mesmas distribuições apresentadas.

Os serviços podem também ser simples ou batch.

O estado pode ser independente: o processo de atendimento não depende do número de clientes esperando pelo serviço. Em contrapartida, em um estado dependente, o processo de atendimento muda de acordo com o número de clientes na fila. Por exemplo, um servidor pode trabalhar mais rápido quando a fila aumenta ou, ao contrário, ficar confuso e então mais lento.

Da mesma forma que no processo de chegada, o padrão de serviço pode variar de acordo com o tempo. Por exemplo, a experiência adquirida com o serviço pode aumentar a produtividade; o cansaço, por outro lado, pode diminuí-la. Caso não haja variação o padrão é estacionário.

Um centro de atraso

Multiservidor com fila única

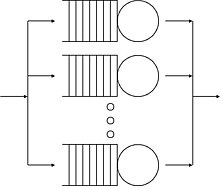Servidor paralelo

Capacidade do sistema

Representa o número máximo de clientes que o sistema suporta, incluindo os que estão em espera e os que estão sendo atendidos. A capacidade pode ser infinita (mais fácil de analisar) ou finita (por exemplo, número limitado de buffers em um roteador). Se a capacidade for finita, quando o sistema estiver lotado nenhum cliente pode entrar até que um cliente saia do sistema, liberando espaço.

População de usuários

Esse componente indica o número potencial de clientes que podem chegar a um sistema. Pode ser finita ou infinita.

Disciplina de atendimento

Exemplo da disciplina de atendimento FIFO (first in first out).

Descreve a forma como os clientes saem da fila de espera para serem atendidos. Algumas disciplinas são:

FIFO (First In, First Out): Primeiro a Entrar, Primeiro a Sair). Disciplina mais comum, inclusive na vida diária. de FCFS (First Come, First Served): Primeiro a Chegar, Primeiro a ser Atendido.]
LIFO (Last In, First Out): Último a Chegar, Primeiro a Sair. Aplicável em sistemas em que o item mais recente é mais fácil de ser recuperado, como por exemplo em sistemas de controle de estoque. de LCFS (Last Come, First Served): Último a chegar, Primeiro a ser Atendido]
Fila com prioridade: a cada cliente é atribuída uma prioridade; clientes com maior prioridade têm preferência no atendimento. Pode ser de dois tipos:
- Preemptivo: o cliente com maior prioridade é atendido imediatamente, interrompendo o atendimento ao cliente com menor prioridade. Ao terminar, o cliente de menor prioridade volta a ser atendido, podendo continuar o processo de onde parou ou então reiniciá-lo
- Não-preemptivo: o cliente com maior prioridade é colocado no início da fila, recebendo o serviço somente quando o cliente em atendimento sai do sistema, mesmo se este for de prioridade mais baixa
Round-robin (algoritmo): cada cliente recebe uma fatia de tempo do servidor (quantum), dentro da qual é atendido. Após o término do quantum, se a atividade não foi completada, o cliente é retirado e outro passa a ser atendido. Posteriormente, o cliente que foi interrompido retorna ao servidor e continua a sua atividade. É muito comum em escalonamento de processos da CPU.
SIRO (Serve In Random Order): Atendimento em Ordem Aleatória. Indenpendente de um item ser recente ou estar na fila há mais tempo, as chances de cada um são as mesmas, enfim, a cada momento, um dos itens da fila será selecionado aleatoriamente.

Notação

As seis características apresentadas acima descrevem um sistema de filas. Para simplificar, utiliza-se a notação de Kendall, proposta em 1953, composta por uma série de símbolos da seguinte forma:

A/S/m/K/N/Q

Em que:

A: Distribuição dos tempos entre as chegadas (Processo de chegada)
S: Distribuição dos tempos de serviço
m: Número de servidores
K: Capacidade do sistema
N: Tamanho da população
Q: Disciplina de atendimento

Exemplos de sistemas de filas

M/G/4/50/2000/LCFS
- Processo de chegada exponencial (Markoviano) ou de Poisson
- Distribuição dos tempos de serviço arbitrária (Geral)
- Quatro servidores
- Capacidade para cinquenta clientes
- População de dois mil clientes
- Disciplina de atendimento "Último a Chegar, Primeiro a ser Servido"

D/M/1/ ∞ {\displaystyle \infty } / ∞ {\displaystyle \infty } /RR
- Processo de chegada determinístico
- Distribuição dos tempos de serviço exponencial (Markoviano) ou de Poisson
- Um servidor
- Capacidade ilimitada
- População infinita
- Disciplina de atendimento Round-robin

Muitas vezes, os três últimos símbolos são omitidos. Nestes casos, assume-se capacidade ilimitada, população infinita e disciplina de atendimento FCFS.

Exemplo:

M/M/1

Distribuições de probabilidade

Exponencial (M)
Uniforme (U)
Arbitrária ou Geral (G)
Erlang ( E k {\displaystyle E_{k}} $E_{k}$ )
Hiperexponencial ( H k {\displaystyle H_{k}} $H_{k}$ )

Leis operacionais

São relações simples que não necessitam de nenhuma hipótese sobre as distribuições dos tempos de serviço ou dos intervalos entre chegadas. Foram identificadas inicialmente por Buzen em 1976 e posteriormente estendidas por Denning e Buzen em 1978.

Quantidades operacionais

São quantidades que podem ser medidas diretamente durante um período finito de observação.

Período de observação: T {\displaystyle T} $T$
Número de chegadas (arrivals): A i {\displaystyle A_{i}} $A_{i}$
Número de términos (completions): C i {\displaystyle C_{i}} $C_{i}$
Tempo ocupado (busy time): B i {\displaystyle B_{i}} $B_{i}$
Taxa de chegada: λ i = A i T {\displaystyle \lambda _{i}={A_{i} \over T}} $\lambda _{i}={A_{i} \over T}$
Vazão (throughput): X i = C i T {\displaystyle X_{i}={C_{i} \over T}} $X_{i}={C_{i} \over T}$
Utilização: U i = B i T {\displaystyle U_{i}={B_{i} \over T}} $U_{i}={B_{i} \over T}$
Tempo médio de serviço: S i = B i C i {\displaystyle S_{i}={B_{i} \over C_{i}}} $S_{i}={B_{i} \over C_{i}}$

Essas quantidades são variáveis que podem mudar de um período de observação para outro. As relações, porém, continuam válidas.

Lei da Utilização

U i = B i T = C i T × B i C i {\displaystyle U_{i}={B_{i} \over T}={C_{i} \over T}\times {B_{i} \over C_{i}}} $U_{i}={B_{i} \over T}={C_{i} \over T}\times {B_{i} \over C_{i}}$

U i = X i S i {\displaystyle U_{i}=X_{i}S_{i}} $U_{i}=X_{i}S_{i}$

Lei de Little

Desenvolvida por John Little no início dos anos 60, A Lei de Little relaciona o número de clientes no sistema com o tempo médio despendido no sistema.

Q i = λ i R i {\displaystyle Q_{i}=\lambda _{i}R_{i}} $Q_{i}=\lambda _{i}R_{i}$

Número médio de clientes = Taxa de chegada x Tempo médio de resposta
R i = S i + W i {\displaystyle R_{i}=S_{i}+W_{i}}
- Tempo médio de resposta = Tempo médio de serviço + Tempo médio de espera

A Lei de Little se aplica sempre que o número de chegadas é igual ao número de saídas (denominado sistema em equilíbrio). Pode ser aplicada também em subsistemas (caixa preta).

Se o sistema está em equilíbrio, a taxa de chegada é igual ao throughput, portanto:

Q i = X i R i {\displaystyle Q_{i}=X_{i}R_{i}} $Q_{i}=X_{i}R_{i}$

Lei do Fluxo Forçado

Relaciona o throughput global do sistema com o throughput dos dispositivos individuais.

Seja V i {\displaystyle V_{i}} $V_{i}$ o número médio de visitas ao recurso i por uma tarefa. Cada pedido que termina precisa passar, em média, V i {\displaystyle V_{i}} $V_{i}$ vezes pelo recurso i. Se X pedidos forem concluídos por unidade de tempo, então V i X {\displaystyle V_{i}X} $V_{i}X$ pedidos terão passado pelo recurso i:

X i = V i X {\displaystyle X_{i}=V_{i}X} $X_{i}=V_{i}X$

Esta lei é aplicável sempre qua a hipótese do sistema em equilíbrio for verdadeira.

Lei da Demanda de Serviço

Combinando as leis da Utilização e do Fluxo Forçado, obtém-se:

U i = X i S i = X V i S i {\displaystyle U_{i}=X_{i}S_{i}=XV_{i}S_{i}} $U_{i}=X_{i}S_{i}=XV_{i}S_{i}$

U i = X D i {\displaystyle U_{i}=XD_{i}} $U_{i}=XD_{i}$

onde D i = V i S i {\displaystyle D_{i}=V_{i}S_{i}} $D_{i}=V_{i}S_{i}$ é a demanda total de serviço no i-ésimo dispositivo.

O dispositivo com a maior demanda de serviço tem a maior utilização, podendo tornar-se um gargalo no sistema.

Lei Geral do Tempo de Resposta

Sistemas de tempo compartilhado podem ser divididos em dois subsistemas: subsistema de terminais e subsistema de central de processamento. Dados os comprimentos individuais Q i {\displaystyle Q_{i}} $Q_{i}$ das filas de cada terminal, pode-se determinar Q {\displaystyle Q} $Q$ :

Q = Q 1 + Q 2 + ⋯ + Q , {\displaystyle Q=Q_{1}+Q_{2}+\cdots +Q_{,}} $Q=Q_{1}+Q_{2}+\cdots +Q_{,}$

X R = X 1 R 1 + X 2 R 2 + ⋯ + X M R M {\displaystyle XR=X_{1}R_{1}+X_{2}R_{2}+\cdots +X_{M}R_{M}} $XR=X_{1}R_{1}+X_{2}R_{2}+\cdots +X_{M}R_{M}$

Dividindo ambos os lados por X e aplicando a Lei do Fluxo Forçado:

R = V 1 R 1 + V 2 R 2 + ⋯ + V M R M {\displaystyle R=V_{1}R_{1}+V_{2}R_{2}+\cdots +V_{M}R_{M}} $R=V_{1}R_{1}+V_{2}R_{2}+\cdots +V_{M}R_{M}$

R = ∑ i = 1 M R i V i {\displaystyle R=\sum _{i=1}^{M}R_{i}V_{i}} $R=\sum _{i=1}^{M}R_{i}V_{i}$

Lei do Tempo de Resposta Interativo

Em um sistema interativo, usuários geram pedidos que são processados por um subsistema central e os resultados são devolvidos ao terminal. Entre cada pedido de um usuário, há um tempo ocioso Z.

Aplicando-se a Lei de Little ao subsistema central, tem-se:

Q = X R {\displaystyle Q=XR} $Q=XR$

Aplicando-a aos M terminais:

M ¯ = X Z {\displaystyle {\bar {M}}=XZ} ${\bar {M}}=XZ$

Considerando que um cliente ou está sendo atendido ou está ocioso:

M = Q + M ¯ = X R + X Z = X ( R + Z ) {\displaystyle M=Q+{\bar {M}}=XR+XZ=X(R+Z)} $M=Q+{\bar {M}}=XR+XZ=X(R+Z)$

R = M X − Z {\displaystyle R={M \over X}-Z} $R={M \over X}-Z$

Referências

↑ a b «Introduction to Queuing». staff.um.edu.mt. Consultado em 22 de agosto de 2019
↑ «Queue Structure». Business Jargons (em inglês). 30 de dezembro de 2015. Consultado em 22 de agosto de 2019

Bibliografia

Professores da Universidade Federal do Maranhão:

Dr. José de Ribamar Braga Pinheiro Júnior
Dr. Mário Antonio Meireles Teixeira

Ver também

v d e Teoria das filas
Nódulos de fila única	Fila D/M/1 FIla M/D/1 Fila M/D/c Fila M/M/1 Teorema de Burke Fila M/M/c Fila M/M/∞ Fila M/G/1 Fórmula de Pollaczek–Khinchine Método da matriz analítica Fila M/G/k Fila G/M/1 Fila G/G/1 Fórmula de Kingman Equação de Lindley Fila fork–join queue Fila bulk
Processos de chegada	Processo de Poisson Processo de chegada markoviano Processo de chegada racional
Redes de filas	Rede de Jackson Equações de tráfego Teorema de Gordon–Newell Análise de valor médio Algoritmo de Buzen Rede de Kelly Rede-G Rede BCMP
Políticas de serviços	FIFO LIFO Processor sharing Shortest job first Shortest remaining time
Conceitos chave	Corrente de Markov de tempo contínuo Notação de Kendall Lei de Little Solução produto-forma Equação de balanço Quaserreversibilidade Método de servidor flow-equivalent Teorema da chegada Método da decomposição Método de Beneš
Teoremas de limite	Limite de fluido Teoria de campo médio Aproximação em tráfego pesado Movimento browniano refletido
Extensões	Lista de fluidos Rede de filas com camadas Sistema de votação (teoria das filas) Rede de filas adversárias Perda de rede Fila de novo julgamento

v d e
Tempo discreto	Cadeias de Markov Passeio aleatório Autoevitante Processo de Bernoulli Processo de Galton–Watson Processo de Moran Variáveis aleatórias independentes e identicamente distribuídas
Tempo contínuo	Processo de Bessel Movimento browniano Ponte Excursão Fracionário Geométrico Meander Processo de Cauchy Processo de Cox Processo de Feller Processo de Fleming–Viot Processo de Hunt Difusão de Itô Processo de Itô Processo Lévy Tempo local Processo aditivo de Markov Processo de McKean–Vlasov Processo Ornstein–Uhlenbeck Processo de Poisson Evolução de Schramm–Loewner Processo de Wiener Processo de nascimento e morte Processo de contato Passeio aleatório de tempo contínuo Processo empírico Difusão de salto
Ambos	Processo gaussiano Modelo Galves-Löcherbach Cadeias estocásticas com memória de alcance variável Modelo oculto de Markov Processo de Markov Martingale Ruído branco Processo regenerativo
Campos e outros	Processo de Dirichlet Medida de Gibbs Modelo de Hopfield Modelo de Ising Modelo de Potts Campo aleatório de Markov Processo de Pitman–Yor Grafo aleatório
Modelos de série temporal	Modelos ARCH ARIMA ARMA
Modelos financeiros	Black–Derman–Toy Black–Karasinski Chen Cox–Ingersoll–Ross (CIR) Garman–Kohlhagen Heath–Jarrow–Morton (HJM) Heston Ho–Lee Hull–White LIBOR market Rendleman–Bartter SABR volatility Vašíček Wilkie
Modelos atuariais	Bühlmann Cramér–Lundberg Sparre–Anderson
Modelos de filas	Fila M/M/1
Propriedades	Càdlàg Processo contínuo de Feller Gauss–Markov Markov Contínuo Reversível no tempo
Teoremas limites	Teorema central do limite Teorema de Donsker Teoria ergódica Teorema de Fisher–Tippett–Gnedenko Lei dos grandes números Lei do logaritmo iterado Teorema de Sanov
Desigualdades	Burkholder–Davis–Gundy Kunita–Watanabe Martingale de Doob
Ferramentas	Fórmula de Cameron–Martin Convergência de variáveis aleatórias Exponencial de Doléans-Dade Teorema da decomposição de Doob–Meyer Fórmula de Dynkin Fórmula de Feynman–Kac Teorema de Girsanov Integral de Itô Lema de Itō Teorema da continuidade de Kolmogorov Teorema da extensão de Kolmogorov Métrica de Lévy–Prokhorov Teorema de Prokhorov Integral de Skorokhod Teorema da representação de Skorokhod Espaço de Skorokhod Equação diferencial estocástica Tanaka Integral de Stratonovich Espaço de Wiener Clássico Abstrato Princípio da reflexão
Disciplinas	Ciências atuariais Econometria Teoria ergódica Matemática financeira Teoria das probabilidades Teoria das filas Estatística Cálculo estocástico Série temporal Aprendizado de máquina
Categoria:Processos estocásticos