Função gama
| Esta página cita fontes, mas que não cobrem todo o conteúdo. Ajude a inserir referências. Conteúdo não verificável pode ser removido.—Encontre fontes: ABW • CAPES • Google (N • L • A) (Maio de 2012) |
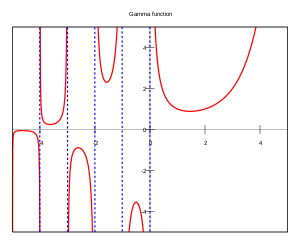 A função gama nos números reais.
A função gama nos números reais.
Em matemática, a função gama (representada pela letra maiúscula grega Γ {\displaystyle \Gamma } ) é uma extensão da função factorial para o conjunto dos números reais e complexos, com o argumento subtraído em 1. Se n é um inteiro positivo define-se da seguinte forma:
Γ ( n + 1 ) = n ! {\displaystyle \Gamma (n+1)=n!} ou Γ ( n ) = ( n − 1 ) ! {\displaystyle \Gamma (n)=(n-1)!}Esta função é estendida por uma continuação analítica (ou extensão analítica) para todos números complexos com, não estando definida apenas nos inteiros não-positivos (em que a função tem polos simples). Portanto, para números complexos com a parte real positiva a definição segue por uma integral imprópria convergente:
Γ ( t ) = ∫ 0 ∞ x t − 1 e − x d x {\displaystyle \Gamma (t)=\int _{0}^{\infty }x^{t-1}e^{-x}dx}Podemos encontrar a demonstração da convergência desta integral no artigo de Emil Artin, The Gamma Function.
A função gama é debutante em diversas funções de distribuição probabilísticas, sendo assim encontra aplicações nos campos da probabilidade, estatística e combinatória.
Motivação
A função gama pode ser vista como solução do seguinte problema de interpolação:
"Encontrar uma curva suave que conecta os pontos (x , y) dados por y = (x − 1)! em que x é um inteiro positivo."
Esboçando em um gráfico os primeiros números fatoriais fica claro que a curva pode ser desenhada, mas seria preferível ter um expressão analítica que descreve precisamente a curva, na qual o número de operações não dependa do tamanho de x. A simples fórmula recursiva para o fatorial x! = x × ... × 2 × 1, não pode ser usada para obter valores fracionários, pois é válida apenas quando x é um número natural. No entanto, foi demonstrado por Euler que não há uma expressão analítica convencional para fatorial, no sentido que não pode ser a combinação finita (com um número finito de termos) de somas, potências, produtos, funções exponenciais e logaritmos, demonstrado em seu artigo intitulado "Sobre progressões transcendentais, nas quais o termo geral não pode ser expresso algebricamente", ("De progressionibus transcendentibus seu quarum termini generales algebraice dari nequeunt"). A função gama é uma solução que não só resolve este problema, mas também possuí distinguíveis propriedades entre as candidatas, como é mostrado no Teorema de Bohr-Mollerup.
Prova
É fácil perceber, através da regra da cadeia e de recursos da integração imprópria, que
∫ 0 ∞ e − r d r = − e − r | 0 ∞ = 1 {\displaystyle \int _{0}^{\infty }e^{-r}\,dr=\left.-e^{-r}\right\vert _{0}^{\infty }=1}Usando o método da substituição, de modo que r = s t , d r = t d s {\displaystyle r=st,dr=tds} , (t>0 e fixo), obtém-se:
∫ 0 ∞ e − s t d s = 1 t , t > 0 {\displaystyle \int _{0}^{\infty }e^{-st}\,ds={\frac {1}{t}},t>0}Derivando-se em relação a t {\displaystyle t} e aplicando a fórmula de Leibniz:
∫ 0 ∞ s e − s t d s = 1 t 2 , t > 0 {\displaystyle \int _{0}^{\infty }se^{-st}\,ds={\frac {1}{t^{2}}},t>0}Utilizando o mesmo processo novamente:
∫ 0 ∞ s 2 e − s t d s = 1.2 t 3 , t > 0 {\displaystyle \int _{0}^{\infty }s^{2}e^{-st}\,ds={\frac {1.2}{t^{3}}},t>0}Derivando sucessivas vezes em relação a t {\displaystyle t} :
∫ 0 ∞ s n e − s t d s = n ! t n + 1 , t > 0 {\displaystyle \int _{0}^{\infty }s^{n}e^{-st}\,ds={\frac {n!}{t^{n+1}}},t>0}Para t = 1 {\displaystyle t=1}
∫ 0 ∞ s n e − s d s = n ! {\displaystyle \int _{0}^{\infty }s^{n}e^{-s}\,ds=n!}Dessa forma, tem-se uma função fatorial definida para quaisquer valores reais positivos x {\displaystyle x} , de modo que:
g ( x ) = ∫ 0 ∞ e − s s x d s = x ! {\displaystyle g(x)=\int _{0}^{\infty }e^{-s}s^{x}\,ds=x!}Contudo, consagrou-se o uso de uma definição levemente destoante, a Função Gama de Euler, tal que
Γ ( x ) = ∫ 0 ∞ e − t t x − 1 d t {\displaystyle \Gamma (x)=\int _{0}^{\infty }e^{-t}t^{x-1}\,dt}Assim,
Γ ( x ) = g ( x − 1 ) {\displaystyle \Gamma (x)=g(x-1)}E, analogamente, para números inteiros,
Γ ( n ) = ( n − 1 ) ! {\displaystyle \Gamma (n)=(n-1)!}Com isso, acabamos de provar que a função gama funciona como uma representação do Fatorial, quando é aplicada em números inteiros, isso permite a idealização de afirmarmos que quando calculamos a função gama para outros números em seu domínio (Números fracionários ou irracionais) estamos obtendo o "fatorial" desses números. Um exemplo disso, é a seguinte relação, da qual omitiremos a demonstração:
( 1 / 2 ) ! = Γ ( 3 2 ) = 1 2 Γ ( 1 2 ) = 1 2 π {\displaystyle (1/2)!=\Gamma \left({\frac {3}{2}}\right)={\frac {1}{2}}\Gamma \left({\frac {1}{2}}\right)={\frac {1}{2}}{\sqrt {\pi }}}A função gama incompleta é obtida pela mesma integral que a função gama, porém com uma integral indefinida no lugar da integral definida:
Γ ( a , x ) = ∫ x ∞ t a − 1 e − t d t . {\displaystyle \Gamma (a,x)=\int _{x}^{\infty }t^{a-1}\,e^{-t}\,dt.} γ ( a , x ) = ∫ 0 x t a − 1 e − t d t . {\displaystyle \gamma (a,x)=\int _{0}^{x}t^{a-1}\,e^{-t}\,dt.}A função digama é a derivada do logaritmo da função gama:
ψ ( x ) = d d x ln Γ ( x ) = Γ ′ ( x ) Γ ( x ) . {\displaystyle \psi (x)={\frac {d}{dx}}\ln {\Gamma (x)}={\frac {\Gamma '(x)}{\Gamma (x)}}.}A função beta, também chamada de Integral de Euler de primeiro tipo, pode ser definida por uma razão de funções gama:
B ( x , y ) = Γ ( x ) Γ ( y ) Γ ( x + y ) {\displaystyle \mathrm {B} (x,y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}}}Propriedades
Propriedade Fundamental
A propriedade mais importante da função gama é dada por
Γ ( z + 1 ) = z Γ ( z ) {\displaystyle \Gamma (z+1)=z\Gamma (z)}Que pode ser obtida pela integração por partes da definição da função gama
Γ ( z + 1 ) = − e − t t z | 0 ∞ + z ∫ 0 ∞ t z − 1 e − t d t {\displaystyle \Gamma (z+1)=\left.-e^{-t}t^{z}\right\vert _{0}^{\infty }+z\int _{0}^{\infty }t^{z-1}e^{-t}dt}O lado esquerdo do resultado é igual a zero. A integral do lado direito do resultado é a própria definição da função gama.
Segue desta propriedade que
Γ ( z ) = ( z − 1 ) Γ ( z − 1 ) {\displaystyle \Gamma (z)=(z-1)\Gamma (z-1)}E também
Γ ( z + 1 ) = z ( z − 1 ) ( z − 2 ) . . . {\displaystyle \Gamma (z+1)=z(z-1)(z-2)...}Para números inteiros, a recursividade da propriedade cai na definição do fatorial. Esta propriedade é válida também para números no domínio dos complexos.
Além delas, existe a importante propriedade abaixo encontrada por Hamilton Brito de forma independente, com a {\displaystyle a} e b {\displaystyle b} ∈ N {\displaystyle \in \mathbb {N} } sendo a ≥ 2 {\displaystyle a\geq 2} e b ≥ 1 {\displaystyle b\geq 1} :
Γ ( a + b i ) ⋅ Γ ( a − b i ) = b ⋅ ( b 2 + 1 ) ⋅ π ⋅ c o s s e c h ( b ⋅ π ) ∏ n = 2 a − 1 ( b 2 + n 2 ) {\displaystyle \Gamma (a+bi)\cdot \Gamma (a-bi)=b\cdot (b^{2}+1)\cdot \pi \cdot cossech(b\cdot \pi )\prod _{n=2}^{a-1}(b^{2}+n^{2})}
Representação em produto
A função gama pode ser escrita por um produto de Hadamard:
Γ ( z ) = e − γ z z ∏ n = 1 ∞ ( 1 + z n ) − 1 e z n {\displaystyle \Gamma (z)={\frac {e^{-\gamma z}}{z}}\prod _{n=1}^{\infty }\left(1+{\frac {z}{n}}\right)^{-1}e^{\frac {z}{n}}}
Domínio da função gama
A integral que define a função gama converge para todo
x > 0 {\displaystyle x>0}Assim um intervalo de definição da função é:
Γ ( x ) : ( 0 , ∞ ) {\displaystyle \Gamma (x):(0,{\infty })} ProvaEscrevendo A função como:
∫ 0 1 t x − 1 e − t d t + ∫ 1 ∞ t x − 1 e − t d t {\displaystyle \int _{0}^{1}t^{x-1}e^{-t}dt+\int _{1}^{\infty }t^{x-1}e^{-t}dt}A segunda integral converge muito rápido pelo fator e − t {\displaystyle e^{-t}} que tende a zero quando t {\displaystyle t} tende a infinito, neutralizando qualquer crescimento que o termo t x − 1 {\displaystyle t^{x-1}} apresente.
Na primeira integral para 0 < t < 1 {\displaystyle 0<t<1} a função e − t {\displaystyle e^{-t}} fica controlada. Logo a convergência dessa integral vai depender apenas do termo t x − 1 {\displaystyle t^{x-1}} .
Para x > 0 {\displaystyle x>0}
∫ 0 1 t x − 1 d t = 1 x x − 0 = 1 x < ∞ {\displaystyle \int _{0}^{1}t^{x-1}dt={\frac {1^{x}}{x}}-0={\frac {1}{x}}<{\infty }}Para x = 0 {\displaystyle x=0}
∫ 0 1 t − 1 d t = l n 1 − l n 0 = ∞ {\displaystyle \int _{0}^{1}t^{-1}dt=ln{1}-ln{0}={\infty }}Para x < 0 {\displaystyle x<0} temos que x − 1 < − 1 {\displaystyle x-1<-1} , então:
∫ 0 1 t x − 1 d t > ∫ 0 1 t − 1 d t = ∞ {\displaystyle \int _{0}^{1}t^{x-1}dt>\int _{0}^{1}t^{-1}dt={\infty }}Pela propriedade fundamental, pode-se estender o domínio da função gama em intervalos que contém números negativos. Define-se então que
Γ ( z ) = Γ ( z + 1 ) z {\displaystyle \Gamma (z)={\frac {\Gamma (z+1)}{z}}}Para números no intervalo z ∈ (-1, 0), como z < 0, vê-se que
Γ ( z ) < 0 {\displaystyle \Gamma (z)<0}E também que
lim z → 0 − Γ ( z ) = lim z → 1 + Γ ( z ) = − ∞ {\displaystyle \lim _{z\to 0^{-}}\Gamma (z)=\lim _{z\to 1^{+}}\Gamma (z)=-\infty }Continuando com o mesmo processo, o domínio da função gama passa a ser
R {\displaystyle \mathbb {R} \,} - {0, -1, -2, -3, ...}Um resultado de interesse em algumas aplicações calculado pela Função é Γ ( 1 2 ) = π {\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}
Demonstração Γ ( 1 2 ) = ∫ 0 ∞ t − ( 1 2 ) e − t d t {\displaystyle \Gamma \left({\frac {1}{2}}\right)=\int _{0}^{\infty }t^{-\left({\frac {1}{2}}\right)}e^{-t}dt}Fazendo t = r 2 {\displaystyle t=r^{2}} , obtemos d t = 2 r d r {\displaystyle dt=2rdr} logo:
∫ 0 ∞ t − ( 1 2 ) e − t d t = 2 ∫ 0 ∞ e − r 2 d r {\displaystyle \int _{0}^{\infty }t^{-\left({\frac {1}{2}}\right)}e^{-t}dt=2\int _{0}^{\infty }e^{-r^{2}}dr}Utilizando a técnica de Liouville:
I = ∫ 0 ∞ e − x 2 d x {\displaystyle I=\int _{0}^{\infty }e^{-x^{2}}dx} I 2 = ∫ 0 ∞ e − x 2 d x ∫ 0 ∞ e − y 2 d y = ∫ 0 ∞ ∫ 0 ∞ e − ( x 2 + y 2 ) d x d y {\displaystyle I^{2}=\int _{0}^{\infty }e^{-x^{2}}dx\int _{0}^{\infty }e^{-y^{2}}dy=\int _{0}^{\infty }\int _{0}^{\infty }e^{-(x^{2}+y^{2})}dxdy}A última integral é uma integral dupla facilmente calculada em coordenadas polares:
I 2 = ∫ 0 π 2 ∫ 0 ∞ e − r 2 r d r d θ = π 4 {\displaystyle I^{2}=\int _{0}^{\frac {\pi }{2}}\int _{0}^{\infty }e^{-r^{2}}rdrd{\theta }={\frac {\pi }{4}}}Utilizando uma troca de variáveis é fácil chegar ao resultado.
I 2 = π 4 {\displaystyle I^{2}={\frac {\pi }{4}}} I = π 2 {\displaystyle I={\frac {\sqrt {\pi }}{2}}} 2 ∫ 0 ∞ e − r 2 d r = 2 π 2 = π {\displaystyle 2\int _{0}^{\infty }e^{-r^{2}}dr=2{\frac {\sqrt {\pi }}{2}}={\sqrt {\pi }}}Sendo assim:
Γ ( 1 2 ) = π {\displaystyle \Gamma \left({\frac {1}{2}}\right)={\sqrt {\pi }}}Referências
- ↑ «Confira este exemplo e faça outros com O Monitor». omonitor.io. Consultado em 19 de março de 2016
Bibliografia
- Boyce e DiPrima. Equações Diferenciais Elementares e Problemas de Valores de Contorno, editora LTC, 9ª edição, 2010.
- Dennis G. Zill, Michael R. Cullen; Equações Diferenciais, vol 1; Editora Makron Books do Brasil
- Davis, Philip J.; Abramowitz, Milton; Stegun, Irene. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. 1972.
Ligações externas
| Funções | ||
|---|---|---|
| Tipos | Analítica • Bijetora • Convexa • Divisor • Elementar • Exponencial • Fatorial • Identidade • Inclusão • Inteira • Inversa • Iterada • Limitada • Integral de Tchebychev • Logaritmo • Logaritmo natural • Monótona • Parcial • Polinomial • Retangular • Simples • Sinal • Sobrejetora • Suave |  |
| Trigonométricas | Seno • Cosseno • Tangente • Cotangente • Secante • Cossecante | |
| Hiperbólicas | Seno hiperbólico • Cosseno hiperbólico • Tangente hiperbólica • Cotangente hiperbólica • Secante hiperbólica • Cossecante hiperbólica | |
| Famosas | Ackermann • Bessel • Dirichlet • Gama • Heaviside • Mertens • Möbius • Weierstrass | |
| Conceitos | Assimptota/Assíntota • Curva • Derivada • Espaço funcional • Espaço Lp • Gráficos • Integral • Limite • Injectividade • Parte inteira • Primitiva • Projeção • Reta | |
| Funções em economia | Demanda • Oferta • Utilidade | |
 ) é uma extensão da
) é uma extensão da  ou
Γ
(
n
)
=
(
n
−
1
)
!
{\displaystyle \Gamma (n)=(n-1)!}
ou
Γ
(
n
)
=
(
n
−
1
)
!
{\displaystyle \Gamma (n)=(n-1)!}



 , (t>0 e fixo), obtém-se:
, (t>0 e fixo), obtém-se:

 e aplicando a
e aplicando a 




 , de modo que:
, de modo que:




 γ
(
a
,
x
)
=
∫
0
x
t
a
−
1
e
−
t
d
t
.
{\displaystyle \gamma (a,x)=\int _{0}^{x}t^{a-1}\,e^{-t}\,dt.}
γ
(
a
,
x
)
=
∫
0
x
t
a
−
1
e
−
t
d
t
.
{\displaystyle \gamma (a,x)=\int _{0}^{x}t^{a-1}\,e^{-t}\,dt.}







 e
b
{\displaystyle b}
e
b
{\displaystyle b}
 ∈
N
{\displaystyle \in \mathbb {N} }
∈
N
{\displaystyle \in \mathbb {N} }
 sendo
a
≥
2
{\displaystyle a\geq 2}
sendo
a
≥
2
{\displaystyle a\geq 2}
 e
b
≥
1
{\displaystyle b\geq 1}
e
b
≥
1
{\displaystyle b\geq 1}
 :
:



 Prova
Prova

 que tende a zero quando
t
{\displaystyle t}
que tende a zero quando
t
{\displaystyle t}
 apresente.
apresente.
 a função
e
−
t
{\displaystyle e^{-t}}
a função
e
−
t
{\displaystyle e^{-t}}



 temos que
x
−
1
<
−
1
{\displaystyle x-1<-1}
temos que
x
−
1
<
−
1
{\displaystyle x-1<-1}
 , então:
, então:




 - {0, -1, -2, -3, ...}
- {0, -1, -2, -3, ...}


 , obtemos
d
t
=
2
r
d
r
{\displaystyle dt=2rdr}
, obtemos
d
t
=
2
r
d
r
{\displaystyle dt=2rdr}
 logo:
logo:

 I
2
=
∫
0
∞
e
−
x
2
d
x
∫
0
∞
e
−
y
2
d
y
=
∫
0
∞
∫
0
∞
e
−
(
x
2
+
y
2
)
d
x
d
y
{\displaystyle I^{2}=\int _{0}^{\infty }e^{-x^{2}}dx\int _{0}^{\infty }e^{-y^{2}}dy=\int _{0}^{\infty }\int _{0}^{\infty }e^{-(x^{2}+y^{2})}dxdy}
I
2
=
∫
0
∞
e
−
x
2
d
x
∫
0
∞
e
−
y
2
d
y
=
∫
0
∞
∫
0
∞
e
−
(
x
2
+
y
2
)
d
x
d
y
{\displaystyle I^{2}=\int _{0}^{\infty }e^{-x^{2}}dx\int _{0}^{\infty }e^{-y^{2}}dy=\int _{0}^{\infty }\int _{0}^{\infty }e^{-(x^{2}+y^{2})}dxdy}


 I
=
π
2
{\displaystyle I={\frac {\sqrt {\pi }}{2}}}
I
=
π
2
{\displaystyle I={\frac {\sqrt {\pi }}{2}}}
 2
∫
0
∞
e
−
r
2
d
r
=
2
π
2
=
π
{\displaystyle 2\int _{0}^{\infty }e^{-r^{2}}dr=2{\frac {\sqrt {\pi }}{2}}={\sqrt {\pi }}}
2
∫
0
∞
e
−
r
2
d
r
=
2
π
2
=
π
{\displaystyle 2\int _{0}^{\infty }e^{-r^{2}}dr=2{\frac {\sqrt {\pi }}{2}}={\sqrt {\pi }}}
